
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求证:当![]() 时,对任意
时,对任意![]() 都有
都有![]() ;
;
(2)若函数![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)
【解析】试题分析:(1)![]() ,令
,令![]() ,求导得
,求导得![]() 单调递减,
单调递减, ![]() 单调递增,
单调递增, ![]() ,即
,即![]() ;(2)令
;(2)令![]() ,则
,则![]() 有两个变号零点,且
有两个变号零点,且![]() ,通过分类讨论得,
,通过分类讨论得,  .
.
试题解析:
(1)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 显然成立;
显然成立;
当![]() 时,
时, ![]() ;
;
令![]() ,
, ![]() ,则
,则![]() ,
,
可得![]() ,
, ![]() ,
, ![]() 减;
减; ![]() ,
, ![]() ,
, ![]() 增;
增;
故![]() 时,
时, ![]() ,
,
综上,任意![]() 都有
都有![]() ,得证.
,得证.
(2)函数定义域为![]() ,令
,令![]() ,若
,若![]() 有两个极值点,则
有两个极值点,则![]() 有两个变号零点,且
有两个变号零点,且![]() ,
,
当![]() 时,
时, ![]() 在
在![]() 上恒成立,函数
上恒成立,函数![]() 在
在![]() 上单增,
上单增, ![]() 至多有一个零点,此时
至多有一个零点,此时![]() 不存在两个极值点;
不存在两个极值点;
当![]() 时,令
时,令![]() ,可得
,可得![]() ,且
,且![]() ,
,
![]() ,即函数
,即函数![]() 在
在![]() 单减,在
单减,在![]() 单增,
单增,
若条件成立,则必有![]()
![]() ,此时
,此时![]() ,
,
下证: ![]() 时,函数
时,函数![]() 有两个零点
有两个零点
由于![]() ,故
,故![]() ,即
,即![]() 在
在![]() 有唯一零点,记为
有唯一零点,记为![]() ;
;
易得![]() 时,
时, ![]() ,且
,且![]()
![]() ,
,
令![]() ,则
,则![]() ,由(1)可得大于0恒成立,从而
,由(1)可得大于0恒成立,从而![]() ,
,
即![]() ,故
,故![]() 在
在![]() 有唯一零点,记为
有唯一零点,记为![]() ,
,
从而, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]()
综上,函数![]() 有两个极值点时,
有两个极值点时,  .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】下图为某校数学专业N名毕业生的综合测评成绩(百分制)频率分布直方图,已知80-90分数段的学员数为21人。

(1)求该专业毕业总人数N和90-95分数段内的人数![]() ;
;
(2)现欲将90-95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n人中仅有两名男生,求安排结果至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量, ![]() 获得本场比赛胜利,最终人机大战总比分定格
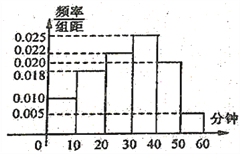
获得本场比赛胜利,最终人机大战总比分定格![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(Ⅰ)根据已知条件完成下面的列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名淡定生中的“围棋迷”人数为![]() 。若每次抽取的结果是相互独立的,求
。若每次抽取的结果是相互独立的,求![]() 的平均值和方差.
的平均值和方差.
附: 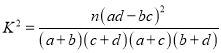 ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取![]() 次.记录如下:
次.记录如下:
甲: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
乙: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(![]() )用茎叶图表示这两组数据.
)用茎叶图表示这两组数据.
(![]() )现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为派哪位学生参加合适?请说明理由.
)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为派哪位学生参加合适?请说明理由.
(![]() )若将频率视为概率,对甲同学在今后的三次数学竞赛成绩进行预测,记这
)若将频率视为概率,对甲同学在今后的三次数学竞赛成绩进行预测,记这![]() 次成绩中高于
次成绩中高于![]() 分的次数为
分的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市甲水厂每天生产![]() 万吨的生活用水,其每天固定生产成本为
万吨的生活用水,其每天固定生产成本为![]() 万元,居民用水的税费价格为每吨
万元,居民用水的税费价格为每吨![]() 元,该市居民每天用水需求量是在
元,该市居民每天用水需求量是在![]() (单位:万吨)内的随机数,经市场调查,该市每天用水需求量的频率分布直方图如图所示,设
(单位:万吨)内的随机数,经市场调查,该市每天用水需求量的频率分布直方图如图所示,设![]() (单位:万吨,
(单位:万吨, ![]() )表示该市一天用水需求量
)表示该市一天用水需求量![]() (单位:万元)表示甲水厂一天销售生活用水的利润(利润=税费收入-固定生产成本),注:当该市用水需求量超过
(单位:万元)表示甲水厂一天销售生活用水的利润(利润=税费收入-固定生产成本),注:当该市用水需求量超过![]() 万吨时,超过的部分居民可以用其他水厂生产的水,甲水厂只收成本厂供应的税费,该市每天用水需求量的概率用频率估计.
万吨时,超过的部分居民可以用其他水厂生产的水,甲水厂只收成本厂供应的税费,该市每天用水需求量的概率用频率估计.
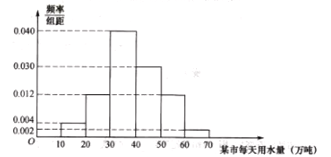
(1)求![]() 的值,并直接写出
的值,并直接写出![]() 表达式;
表达式;
(2)求甲水厂每天的利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为
的距离为![]() ,以
,以![]() 为圆心且与抛物线准线
为圆心且与抛物线准线![]() 相切的圆恰好过原点
相切的圆恰好过原点![]() .点
.点![]() 是
是![]() 与
与![]() 轴的交点,
轴的交点, ![]() 两点在抛物线上且直线
两点在抛物线上且直线![]() 过
过![]() 点,过
点,过![]() 点及
点及![]() 的直线交抛物线于
的直线交抛物线于![]() 点.
点.
(1)求抛物线![]() 的方程;
的方程;
(2)求证:直线![]() 过一定点,并求出该点坐标.
过一定点,并求出该点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com