
【题目】在极坐标系中,已知某曲线C的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求该曲线C的直角坐标系方程及离心率![]()
(2)已知点![]() 为曲线C上的动点,求点
为曲线C上的动点,求点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 知曲线C的极坐标方程为
知曲线C的极坐标方程为![]() 可化为直角坐标系方程
可化为直角坐标系方程![]() ,由于在椭圆方程中
,由于在椭圆方程中![]() ,故可求出离心率;(2)因为直线
,故可求出离心率;(2)因为直线![]() 的极坐标方程为
的极坐标方程为![]() ,所以直线
,所以直线![]() 的直角坐标系方程为
的直角坐标系方程为![]() ,方法一:因为曲线C的参数方程为
,方法一:因为曲线C的参数方程为![]() 为参数),所以可设点
为参数),所以可设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为
的距离为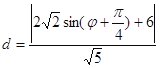 ,所以当
,所以当![]() ,即
,即![]() 时,
时,![]() .方法二:设与直线
.方法二:设与直线![]() 平行且与曲线C相切的直线为
平行且与曲线C相切的直线为![]() ,联立
,联立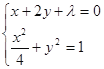 消去
消去![]() 整理得
整理得![]() ,令
,令![]() 得
得![]() ,当
,当![]() 时,切点
时,切点![]() 到直线
到直线![]() 的距离最大.
的距离最大.
试题解析:解:(1)由![]() 知曲线C的极坐标方程为
知曲线C的极坐标方程为![]() 可化为直角坐标系方程
可化为直角坐标系方程![]() 即
即![]() ..3分
..3分
由于在椭圆方程中![]() ..4分
..4分
故离心率![]() ..6分
..6分
(2)因为直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
所以直线![]() 的直角坐标系方程为
的直角坐标系方程为![]() ..8分
..8分
法一:因为曲线C的参数方程为![]() 为参数),所以可设点
为参数),所以可设点![]() 的坐标为
的坐标为![]() ..9分
..9分
则点![]() 到直线
到直线![]() 的距离为
的距离为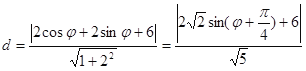 ..11分
..11分
所以当![]() ..12分
..12分
即![]() 时,
时,![]() ..13分
..13分
法二:设与直线![]() 平行且与曲线C相切的直线为
平行且与曲线C相切的直线为![]() ..8分
..8分
联立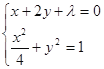 消去
消去![]() 整理得
整理得![]() ..10分
..10分
则![]() ,令
,令![]() 得
得![]() ..11分
..11分
当![]() 时,切点
时,切点![]() 到直线
到直线![]() 的距离最大为
的距离最大为![]() ..13分.
..13分.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查,调查问卷共10道题,答题情况如下表所示.
(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(2)从答对题目数小于8的出租车司机中任选出2人做进一步的调查,求选出的2人中至少有一名女出租车司机的概率.
答对题目数 | [0,8) | 8 | 9 | 10 |
女 | 2 | 13 | 12 | 8 |
男 | 3 | 37 | 16 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=![]() ﹣p
﹣p
④回归直线一定过样本点的中心(![]() ).
).
其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列![]() 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1-![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:
喜欢中国古典文学 | 不喜欢中国古典文学 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢中国古典文学与性别有关?请说明理由;
的把握认为喜欢中国古典文学与性别有关?请说明理由;
(3)已知在喜欢中国古典文学的10位男生中,![]() ,
,![]() ,
,![]() 还喜欢数学,
还喜欢数学,![]() ,
,![]() 还喜欢绘画,
还喜欢绘画,![]() ,
,![]() 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求
还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
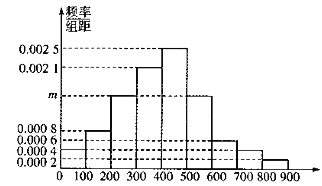
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
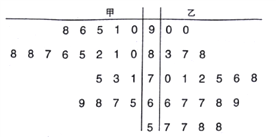
(1)学校规定:成绩不低于75分的为优秀,请填写下面的![]() 联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
联表,并判断有多大把握认为“成绩优秀与教学方式有关”.

附:参考公式及数据

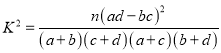
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设![]() 为抽取成绩不低于95分同学人数,求
为抽取成绩不低于95分同学人数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com