
【题目】如图是某几何体的三视图,则该几何体的体积为( )
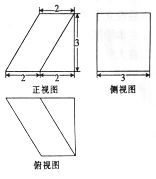
A. 12 B. 15 C. 18 D. 21
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O![]() 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
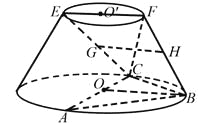
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=
AC=![]() ,AB=BC.求二面角
,AB=BC.求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点,若正方体的棱长为![]() ,求这三个球的表面积.
,求这三个球的表面积.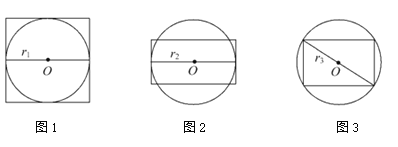
查看答案和解析>>
科目:高中数学 来源: 题型:
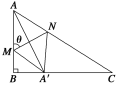
【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,且x=-1处取得极大 值2.
为奇函数,且x=-1处取得极大 值2.
(1)求f(x)的解析式;
(2)过点A(1,t) ![]() 可作函数f(x)图像的三条切线,求实数t的取值范围;
可作函数f(x)图像的三条切线,求实数t的取值范围;
(3)若![]() 对于任意的
对于任意的![]() 恒成立,求实数m取值范围.
恒成立,求实数m取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图(如图甲)和频率分布直方图(如图乙)都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.(注:直方图中
,据此解答如下问题.(注:直方图中![]() 与
与![]() 对应的长方形的高度一样)
对应的长方形的高度一样)
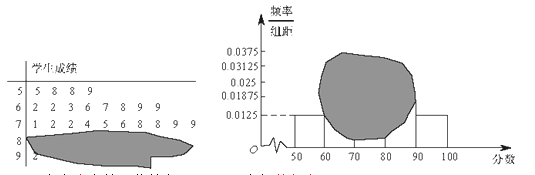
(1)若按题中的分组情况进行分层抽样,共抽取![]() 人,那么成绩在
人,那么成绩在![]() 之间应抽取多少人?
之间应抽取多少人?
(2)现从分数在![]() 之间的试卷中任取
之间的试卷中任取![]() 份分析学生失分情况,设抽取的试卷分数在
份分析学生失分情况,设抽取的试卷分数在![]() 之间 份数为
之间 份数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切,设点
相切,设点![]() 为圆上一动点,
为圆上一动点, ![]() 轴于
轴于![]() ,且动点
,且动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 与直线
与直线![]() 垂直且与曲线
垂直且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com