
【题目】已知等比数列{an}的各项均为正数,且a2=6,a3+a4=72.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an﹣n(n∈N*),求数列{bn}的前n项和 ![]() .
.
【答案】
(1)解:设等比数列{an}的公比为q,
∵a2=6,a3+a4=72,
∴6q+6q2=72,
即q2+q﹣12=0,
解得q=3或q=﹣4,
∵an>0,∴q>0,
∴q=3,a1= ![]() =2,
=2,
∴an=a1qn﹣1=2×3n﹣1(n∈N*);
(2)∵bn=2×3n﹣1﹣n,
∴Sn=2(1+32+33+…+3n﹣1﹣(1+2+3+…+n)=2× ![]() ﹣
﹣ ![]() =3n﹣1﹣
=3n﹣1﹣ ![]() .
.
【解析】1、由等比数列的通项公式可求得q=3或q=﹣4,根据题意可得∴an=a1qn﹣1=2×3n﹣1(n∈N*);
2、根据已知的通项公式整理可得Sn=一个等比数列求和公式+一个等差数列求和公式。,化简整理可得。
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系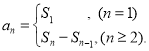 才能正确解答此题.
才能正确解答此题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】定义:在数列 ![]() 中,若
中,若 ![]()
![]() 为常数)则称
为常数)则称 ![]() 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )
①若 ![]() 是“等方差数列”,在数列
是“等方差数列”,在数列 ![]() 是等差数列;
是等差数列;
② ![]() 是“等方差数列”;
是“等方差数列”;
③若 ![]() 是“等方差数列”,则数列
是“等方差数列”,则数列 ![]() 为常)也是“等方差数列”;
为常)也是“等方差数列”;
④若 ![]() 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 m>1 且关于 x 的不等式![]() 的解集为 [0,4] .
的解集为 [0,4] .
①求 m 的值;
②若 a , b 均为正实数,且满足 a+b=m ,求 a2+b2 的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x﹣4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于
=1(a>b>0)的右焦点为F,短轴的一个端点为M,直线l:3x﹣4y=0交椭圆E于A,B两点,若|AF|+|BF|=4,点M到直线l的距离不小于 ![]() ,则椭圆E的离心率的取值范围是( )
,则椭圆E的离心率的取值范围是( )
A.(0, ![]() ]
]
B.(0, ![]() ]
]
C.[ ![]() ,1)
,1)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB=AC=AA1 , ![]() ,点D是BC的中点.
,点D是BC的中点.
(I)求证:AD⊥平面BCC1B1;
(II)求证:A1B∥平面ADC1;
(III)求二面角A﹣A1B﹣D的余弦值.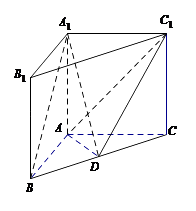
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,其中a10=30,a20=50.
(1)求数列{an}的通项公式;
(2)若bn=an﹣20,求数列{bn}的前n项和Tn的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com