
【题目】莱市在市内主于道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为![]() ,半径为
,半径为![]() ,并与北京路一边所在直线
,并与北京路一边所在直线![]() 相切于点
相切于点![]() .点
.点![]() 为上半圆弧上一点,过点
为上半圆弧上一点,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() .市园林局计划在
.市园林局计划在![]() 内进行绿化,设
内进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),![]() (单位:弧度).
(单位:弧度).

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)当绿化面积![]() 最大时,试确定点
最大时,试确定点![]() 的位置,并求最大面积.
的位置,并求最大面积.
科目:高中数学 来源: 题型:
【题目】如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.

(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
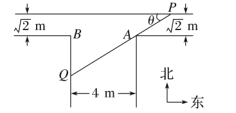
【题目】某“![]() ” 型水渠南北向宽为
” 型水渠南北向宽为![]() ,东西向宽为
,东西向宽为![]() ,其俯视图如图所示.假设水渠内的水面始终保持水平位置.
,其俯视图如图所示.假设水渠内的水面始终保持水平位置.
(1) 过点![]() 的一条直线与水渠的内壁交于
的一条直线与水渠的内壁交于![]() 两点,且与水渠的一边的夹角为
两点,且与水渠的一边的夹角为![]() (
(![]() 为锐角),将线段
为锐角),将线段![]() 的长度
的长度![]() 表示为
表示为![]() 的函数;
的函数;
(2) 若从南面漂来一根长度为![]() 的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?试说明理由.
的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,取相同的长度单位,若曲线
轴正半轴为极轴建立极坐标系,取相同的长度单位,若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),设
为参数),设![]() 是曲线
是曲线![]() 上任一点,
上任一点,![]() 是曲线
是曲线![]() 上任一点.
上任一点.
(1)求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(2)已知直线![]() ,点
,点![]() 在曲线
在曲线![]() 上,求点
上,求点![]() 到
到![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】徐州、苏州两地相距500千米,一辆货车从徐州匀速行驶到苏州,规定速度不得超过100千米/小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为0.01;固定部分为![]() 元(
元(![]() >0).
>0).
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 某个集团公司下属的甲、乙两个企业在2014年1月的产值都为a万元,甲企业每个月的产值与前一个月相比增加的产值相等,乙企业每个月的产值与前一个月相比增加的百分数相等,到2015年1月两个企业的产值再次相等.
(1)试比较2014年7月甲、乙两个企业产值的大小,并说明理由.
(2)甲企业为了提高产能,决定投入3.2万元买台仪器,并且从2015年2月1日起投入使用.从启用的第一天起连续使用,第n天的维修保养费为![]() 元(n∈N*),求前n天这台仪器的日平均耗资(含仪器的购置费),并求日平均耗资最小时使用的天数?
元(n∈N*),求前n天这台仪器的日平均耗资(含仪器的购置费),并求日平均耗资最小时使用的天数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月9-25日,第23届冬奥会在韩国平昌举行.4年后,第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会,某大学在平昌冬奥会开幕后的第二天,从全校学生中随机抽取了120名学生,对是否收看平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根据上表说明,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(Ⅱ)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动.
(ⅰ)问男、女学生各选取多少人?
(ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍,求恰好选到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,![]() 为直角三角形,
为直角三角形,![]() ,且
,且![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com