
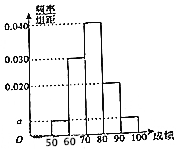
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
分析 (Ⅰ)根据频率和为1,列方程求出a的值;
(Ⅱ)由频率分布直方图计算晋级成功的频率,填写列联表,计算观测值K2,对照临界值得出能有85%的把握认为“晋级成功”与性别有关;
(Ⅲ)由晋级失败的频率估计概率,得X~B(4,$\frac{3}{4}$),计算对应的概率,写出X的分布列,计算数学期望值.
解答 解:(Ⅰ)根据频率和为1,列方程得:
(2a+0.020+0.030+0.040)×10=1,
解得a=0.005;
(Ⅱ)由频率分布直方图知,晋级成功的频率为0.20+0.05=0.25;
填写列联表如下,
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | 34 | 50 |
| 女 | 9 | 41 | 50 |
| 合计 | 25 | 75 | 100 |
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{256}$ | $\frac{3}{64}$ | $\frac{54}{256}$ | $\frac{108}{256}$ | $\frac{81}{256}$ |
点评 本题考查了频率分布直方图与独立性检验的问题,也考查了离散型随机变量的分布列与数学期望的计算问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$p,0) | B. | (-2$\sqrt{3}$p,0) | C. | (-$\frac{\sqrt{3}p}{3}$,0) | D. | (-$\frac{2\sqrt{3}p}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 10 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知x的取值范围是[0,8],执行如图的程序框图,则输出的y≥3的概率为( )
已知x的取值范围是[0,8],执行如图的程序框图,则输出的y≥3的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com