
是否存在常数 ,使等式
,使等式 对于一切
对于一切 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
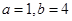 ,证明详见解析.
,证明详见解析.
解析试题分析:先从特殊情形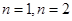 ,等式必须成立,求出
,等式必须成立,求出 值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
试题解析:若存在常数 使等式成立,则将
使等式成立,则将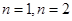 代入上式,有
代入上式,有 得
得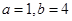 ,即有
,即有 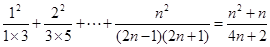 对于一切
对于一切 成立. 5分
成立. 5分
数学归纳法证明如下:
证明如下:(1)当 时,左边=
时,左边=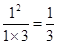 ,右边=
,右边= ,所以等式成立,
,所以等式成立,
(2)假设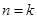 (
( 且
且 )时等式成立,即
)时等式成立,即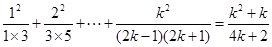 ,
,
当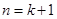 时,
时,

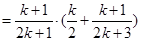
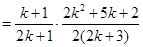


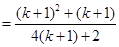
也就是说,当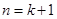 时,等式成立,
时,等式成立,
综上所述,可知等式对任何 都成立. 12分
都成立. 12分
考点:数学归纳法.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:填空题
将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥
的侧面和底面分别叫直角三棱锥的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.已知直角三角形具有性质:“斜边的中线长等于斜边边长的一半”.仿照此性质写出直角三棱锥具有的性质: .
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)已知a>b>c,且a+b+c=0,用分析法求证:<a.
(2)f(x)=,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求 +
+ +
+ +…+
+…+ 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对于命题:如果 是线段
是线段 上一点,则
上一点,则 ;将它类比到平面的情形是:若
;将它类比到平面的情形是:若 是△
是△ 内一点,有
内一点,有 ;将它类比到空间的情形应该是:若
;将它类比到空间的情形应该是:若 是四面体
是四面体 内一点,则有__________________________.
内一点,则有__________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下面给出了关于复数的三种类比推理:
(1)复数的加减法运算法则可以类比多项式的加减法运算法则;
(2)由向量 的性质
的性质 =
= 类比得到复数
类比得到复数 的性质
的性质 ;
;
(3)由向量加法的几何意义可以类比得到复数的加法的几何意义。
其中类比错误的是___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com