
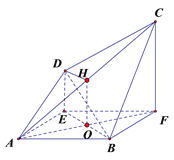
【题目】如图1,在高为2的梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .已知
.已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]()
同侧折起,使得![]() ,
,![]() ,得空间几何体
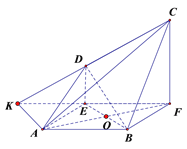
,得空间几何体![]() ,如图2.
,如图2.


(Ⅰ)证明:![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
试题分析:
(Ⅰ)连接![]() 交
交![]() 于
于![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 是
是![]() 的中位线,结合已知从而可得平行四边形
的中位线,结合已知从而可得平行四边形![]() ,因此有
,因此有![]() ,于是由线面平行的判定定理得线面平行;
,于是由线面平行的判定定理得线面平行;
(Ⅱ)关键是顶点的转化,由线面平行有![]()
![]()
![]()
![]() ,则体积可得.
,则体积可得.
试题解析:
(Ⅰ)证法一:连接![]() 交
交![]() 于
于![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]()
是![]() 的中位线,所以
的中位线,所以![]() .
.
由已知得![]() ,所以
,所以![]() ,连接
,连接![]() ,
,
则四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又因为![]() 所以
所以![]() ,即
,即![]() .
.
证法二:延长![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
由已知得![]() ,所以
,所以![]() 是
是![]() 的中位线,所以
的中位线,所以![]()
所以![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]()
又因为![]() 所以
所以![]() .
.
证法三:取![]() 的中点
的中点![]() ,连接
,连接![]() ,易得
,易得![]() ,即四边形
,即四边形![]() 是
是
平行四边形,则![]() ,又
,又![]()
所以![]()
又因为![]() ,所以四边形
,所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
又![]() 是平行四边形,所以
是平行四边形,所以![]() ,所以
,所以![]() ,所以
,所以
四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,又又
,又又![]()
所以![]()
又![]() ,所以面
,所以面![]() ,又
,又![]() ,所以
,所以![]() .
.

(Ⅱ)因为![]() ,所以
,所以![]() ,由已知得,四边形ABEF为正方形,且边长为2,则在图2中,AF
,由已知得,四边形ABEF为正方形,且边长为2,则在图2中,AF![]() BE,由已知AF
BE,由已知AF![]() BD,BE
BD,BE![]() BD=B,,可得AF
BD=B,,可得AF![]() 面BDE, 又DE
面BDE, 又DE![]() 面BDE,所以AF
面BDE,所以AF![]() DE,又AE
DE,又AE![]() DE,AF
DE,AF![]() AE=E,所以DE
AE=E,所以DE![]() 面ABEF, 且
面ABEF, 且![]() ,所以
,所以![]() ,所以
,所以![]() 是三棱锥
是三棱锥![]() 的高,四边形
的高,四边形![]() 是直角梯形。
是直角梯形。
![]()


科目:高中数学 来源: 题型:
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
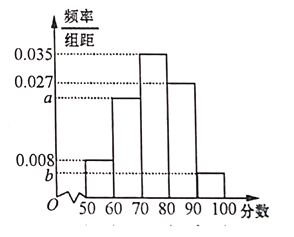
(1)求![]() 的值;
的值;
(2)若按照分层抽样从[50,60),[60,70)中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在[50,60)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
选择全文 | 不选择全文 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
附: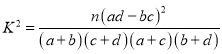 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保险公司统计的资料表明:居民住宅区到最近消防站的距离x(单位:千米)和火灾所造成的损失数额y(单位:千元)有如下的统计资料:
距消防站距离x(千米) | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
火灾损失费用y(千元) | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明y与x有线性相关关系,试求:
(Ⅰ)求相关系数![]() (精确到0.01);
(精确到0.01);
(Ⅱ)求线性回归方程(精确到0.01);
(III)若发生火灾的某居民区与最近的消防站相距10.0千米,评估一下火灾的损失(精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
参考公式:相关系数  ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有学生50人,其中男同学30人,用分层抽样的方法从该班抽取5人去参加某社区服务活动.
(1)求从该班男女同学在各抽取的人数;
(2)从抽取的5名同学中任选2名谈此活动的感受,求选出的2名同学中恰有1名男同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() …是然对数底数.
…是然对数底数.
(1)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,
, ![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求使不等式
时,求使不等式![]() 在一切实数上恒成立的最大正整数
在一切实数上恒成立的最大正整数![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com