
【题目】设![]() 的
的![]() 个子集
个子集![]() 满足:(1)对任意的
满足:(1)对任意的![]() ,
,![]() 恰有奇数个元素;(2)对任意的
恰有奇数个元素;(2)对任意的![]() ,都有
,都有![]() .(3)若
.(3)若![]() ,则
,则![]() .试确定
.试确定![]() 的最大值.
的最大值.
【答案】![]()
【解析】
首先,下列![]() 个集合满足条件(1),(2),(3):
个集合满足条件(1),(2),(3):
![]() ,
,![]() .
.
其次证明:![]() .
.
若不然,设![]() 的
的![]() 个子集
个子集![]() 同时满足(1),(2),(3).
同时满足(1),(2),(3).
称满足(3)的数对![]() 为“搭档”,用
为“搭档”,用![]() 表示集合
表示集合![]() 的元素个数.
的元素个数.
先给出一个引理.
引理在奇数个顶点的图中,必有一个顶点的度数为偶数.
证明略.
回到原题.
(1)若存在![]() ,使得
,使得![]() 为奇数,不妨设
为奇数,不妨设![]() .
.
则对每个![]() ,由题设
,由题设![]() 在
在![]() 中的搭档个数为奇数.
中的搭档个数为奇数.
设![]() 对应的点分别为
对应的点分别为![]() .
.
若![]() 为搭档关系,则在对应的两点之间连一条线.这些点构成的图中每个顶点度数为奇数,由引理,这不可能.
为搭档关系,则在对应的两点之间连一条线.这些点构成的图中每个顶点度数为奇数,由引理,这不可能.
(2)若对任意的![]() ,
,![]() 为偶数,设
为偶数,设![]() .
.
设![]() 为
为![]() 除1之外的搭档构成的集合.则
除1之外的搭档构成的集合.则![]() 为奇数.从而
为奇数.从而![]() 为偶数.
为偶数.
再考虑![]() 这
这![]() 个数,其中必有一个出现在偶数个
个数,其中必有一个出现在偶数个![]() 中(否则,奇数个奇数的和为奇数,即出现的总次数为奇数,与
中(否则,奇数个奇数的和为奇数,即出现的总次数为奇数,与![]() 为偶数矛盾)(设这个数为
为偶数矛盾)(设这个数为![]() ),则1与
),则1与![]() 的公共搭档数为偶数,即
的公共搭档数为偶数,即![]() 为偶数,与假设矛盾.
为偶数,与假设矛盾.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,双曲线
,双曲线![]() 的一条渐近线与
的一条渐近线与![]() 轴所成的夹角为
轴所成的夹角为![]() ,且双曲线的焦距为
,且双曲线的焦距为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
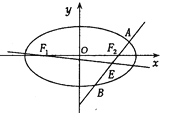
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,过
的左,右焦点,过![]() 作直线
作直线![]() (与
(与![]() 轴不重合)交椭圆于
轴不重合)交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2012位学者参加某数学会议,他们中有些人相互认识,且满足:
(1)每个人至少认识其中的671个人;
(2)对于其中任意两个人![]() 、
、![]() ,若
,若![]() 、
、![]() 相互不认识,则总可以通过其他人间接认识,即存在
相互不认识,则总可以通过其他人间接认识,即存在![]() ,使得
,使得![]() 认识
认识![]() ,
,![]() 认识
认识![]() ,
,![]() 认识
认识![]() ;
;
(3)不可以将2012位学者排成一排,使得相邻的两个人相互认识.
证明:可以将2012位学者分成两组,其中一组能够排成一圈,使得相邻的人相互认识,另一组任何两个人不认识.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)①证明:当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() ;
;
②求实数![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,恒有
,恒有![]() 成立.
成立.
注:![]() 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ;
;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员每次射击命中不低于8环的概率为![]() ,命中8环以下的概率为
,命中8环以下的概率为![]() ,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先用计算器产生0至9之间取整数值的随机数.指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以三个随机数作为一组.代表三次射击的结果,产生如下20组随机数:
,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先用计算器产生0至9之间取整数值的随机数.指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以三个随机数作为一组.代表三次射击的结果,产生如下20组随机数:
524207443815510013429966027954
576086324409472796544917460962
据此估计,该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com