【题目】某学校青年职工、中年职工、老年职工的人数之比为7:5:3，为了了解该单位职工的健康情况，用分层抽样的方法从中抽取样本 ．若样本中的青年职工为14人，则样本容量为______．
口算题卡北京妇女儿童出版社系列答案科目：高中数学 来源： 题型：
【题目】已知A，B是椭圆 
=1和双曲线 
=1的公共顶点，其中a＞b＞0，P是双曲线上的动点，M是椭圆上的动点（P，M都异于A，B），且满足 
=λ（ 
）（λ∈R），设直线AP，BP，AM，BM的斜率分别为k1 ， k2 ， k3 ， k4 ， 若k1+k2= 
，则k3+k4= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1、x2、x3、x4，且x1＜x2＜x3＜x4 ， 则2（x4﹣x1）+（x3﹣x2）的取值范围是（ ）
A.（8，6 
）
B.（6 ，4 
）
C.[8，4 ]
D.（8，4 ]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，圆
的方程为
，以坐标原点为极点，
轴正半轴为极轴建立极坐标系，直线
的参数方程为
（
为参数）
（1）求圆的直角坐标方程和直线的普通方程；
（2）若直线与圆相切，求实数
的值；
查看答案和解析>>
科目：高中数学 来源： 题型：
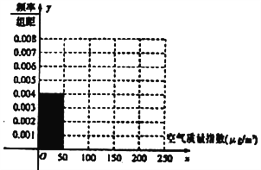
【题目】全世界越来越关注环境保护问题，某监测站点于2018年1月某日起连续
天监测空气质量指数(
)，数据统计如下：
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
（1）根据所给统计表和频率分布直方图中的信息求出，
的值，并完成频率分布直方图；
（2）由频率分布直方图，求该组数据的众数和中位数；
（3）在空气质量指数分别属于
和
的监测数据中，用分层抽样的方法抽取
天，再从中任意选取
天，求事件
“两天空气都为良”发生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|cosx|sinx，给出下列五个说法：
①f（ 
π）=﹣ 
；
②若|f（x1）|=|f（x2）|，则x1=x2+kπ（k∈Z）；
③f（x）在区间[﹣ 
， ]上单调递增；
④函数f（x）的周期为π．
⑤f（x）的图象关于点（ 
，0）成中心对称．
其中正确说法的序号是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
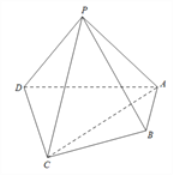
【题目】如图，在四棱锥
中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2， 
.
（1）求证：PD⊥平面PAB；
（2）求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对某交通要道以往的日车流量（单位：万辆）进行统计，得到如下记录：
日车流量x | 0≤x＜5 | 5≤x＜10 | 10≤x＜15 | 15≤x＜20 | 20≤x＜25 | x≥25 |
频率 | 0.05 | 0.25 | 0.35 | 0.25 | 0.10 | 0 |
将日车流量落入各组的频率视为概率，并假设每天的车流量相互独立．
（1）求在未来连续3天里，有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率；
（2）用X表示在未来3天时间里日车流量不低于10万辆的天数，求X的分布列和数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
