
【题目】如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
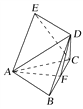
(1)试确定F的位置;
(2)求三棱锥A-CDF的体积.
【答案】(1)F是BC的中点.(2) ![]() .
.
【解析】试题分析:(1)连接BE交AD于点O,取BC的中点F,再根据三角形中位线性质得CE∥OF,最后根据线面平行判定定理得线面平行(2)根据直线BC与平面ABD所成角为30°,可得C到平面ABD的距离,再利用等体积法求三棱锥A-CDF的体积.
试题解析:(1)证明 连接BE交AD于点O,连接OF,
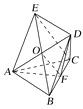
∵CE∥平面ADF,CE平面BEC,平面ADF∩平面BEC=OF,∴CE∥OF.
∵O是BE的中点,∴F是BC的中点.
(2)解 ∵BC与平面ABD所成角为30°,BC=AB=1,
∴C到平面ABD的距离为h=BC·sin 30°=![]() .
.
∵AE=2,∴VA-CDF=VF-ACD=![]() VB-ACD=
VB-ACD=![]() VC-ABD=
VC-ABD=![]() ×
×![]() ×
×![]() ×1×2×
×1×2×![]() =
=![]() .
.


科目:高中数学 来源: 题型:
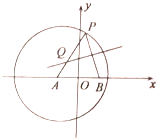
【题目】如图,点![]() 是圆
是圆![]() 内的一个定点,点
内的一个定点,点![]() 是圆
是圆![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,当点
,当点![]() 在圆
在圆![]() 上运动时,点
上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() ,
, ![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 阶“期待数列”:
阶“期待数列”:
①![]() ;
;
②![]() .
.
(![]() )分别写出一个单调递增的
)分别写出一个单调递增的![]() 阶和
阶和![]() 阶“期待数列”.
阶“期待数列”.
(![]() )若某
)若某![]() 阶“期待数列”是等差数列,求该数列的通项公式.
阶“期待数列”是等差数列,求该数列的通项公式.
(![]() )记
)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax-2|.
(1)当a=2时,解不等式f(x)>x+1;
(2)若关于x的不等式f(x)+f(-x)< ![]() 有实数解,求m的取值范围.
有实数解,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司接受了向一地区每天至少运送180 t物资的任务,该公司有8辆载重为6 t的A型卡车和4辆载重为10 t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的费用为A型卡车320元,B型卡车504元,则公司如何调配车辆,才能使公司所花的费用最低,最低费用为________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·山东)设f(x)=xlnx-ax2+(2a-1)x,a∈R.
(1)令g(x)=f′(x),求g(x)的单调区间;
(2)已知f(x)在x=1处取得极大值,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,焦距为2c,且c,
,焦距为2c,且c, ![]() ,2成等比数列.
,2成等比数列.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)点B坐标为(0, ![]() ),问是否存在过点B的直线l交椭圆C于M,N两点,且满足
),问是否存在过点B的直线l交椭圆C于M,N两点,且满足![]() (O为坐标原点)?若存在,求出此时直线l的方程;若不存在,请说明理由.
(O为坐标原点)?若存在,求出此时直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com