
【题目】如图所示,直棱柱![]() 的底面是边长为4的菱形,且
的底面是边长为4的菱形,且![]() ,侧棱长为6,
,侧棱长为6, ![]() ,点
,点![]() 分别是线段
分别是线段![]() 的中点.
的中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() .
.

 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:
【题目】某企业开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名技术人员,将他们随机分成两组,每组20人,第一组技术人员用第一种生产方式,第二组技术人员用第二种生产方式.根据他们完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
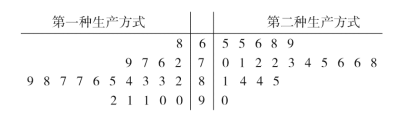
(1)求40名技术人员完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的人数填入下面的列联表:
的人数填入下面的列联表:
超过 | 不超过 | 合计 | |
第一种生产方式 | |||
第二种生产方式 | |||
合计 |
(2)根据(1)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]()
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 1.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
具备以下两个条件:(1)至少有一条对称轴或一个对称中心;(2)至少有两个零点,则称这样的函数为“多元素”函数,下列函数中为“多元素”函数的是_______.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A. 设![]() 是实数,则“
是实数,则“![]() ”是“
”是“![]() ”的充分而不必要条件
”的充分而不必要条件
B. ![]() :“
:“![]() ,
,![]() ”则有
”则有![]() :不存在
:不存在![]() ,
,![]()
C. 命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
D. “![]() ,
,![]() ”为真命题
”为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句是否为命题?如果是,判断它的真假.
(1)这道数学题有趣吗?(2)0不可能不是自然数;(3)![]() ;(4)
;(4)![]() ;
;
(5)91不是素数;(6)上海的空气质量越来越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据如下表:
的样本,得到一周参加社区服务的时间的统计数据如下表:
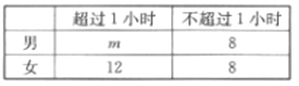
(1)求![]() ,
,![]() ;
;
(2)能否有![]() 的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
附:
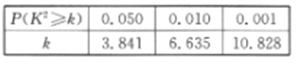
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com