分析:(1)先求函数在x=
处的导数,利用函数在切点处的导数的几何意义是该点处的切线的斜率,求出a值.(2)先求函数的导函数,通过讨论a的范围,讨论函数f(x)的单调性,进而根据函数的单调性和极值求函数的最小值
解答:解:(1)∵f′(x)=2xln(ax)+x
2•
=x[2ln(ax)+1],
∴3e=f′(
)=
[2ln(a•
)+1],
解得a=1.
(2)由题知x>0,f′(x)=x[2ln(ax)+1],
令f′(x)=0,则2ln(ax)+1=0,得x=
,
①当a≥1时,
≤
.
当x∈[
,
]时,f′(x)≥0,
∴f(x)在[
,
]上是增函数,
∴[f(x)]
min=f(
)=
ln
=
(lna-
);
②当
<a<1时,
<
<
.
当x∈[
,
)时,f′(x)<0;
当x∈[
,
]时,f′(x)>0,
∴f(x)在[
,
]上是减函数,在[
,
]上为增函数,
∴[f(x)]
min=f(
)=
ln
=-
;
③当0<a≤
时,
≥
.
当x∈[
,
]时,f′(x)<0,
∴f(x)在[
,
]上是减函数,
∴[f(x)]
min=f(
)=elna
=e(lna+
).
综上所述:当a≥1时,f(x)在[
,
]上的最小值为
(lna-
);
当
<a<1时,f(x)在[
,
]上的最小值为-
;
当0<a≤
时,f(x)在[
,
]上的最小值为e(lna+
).
点评:本题考查了导数的运算及其几何意义,利用导数求函数在闭区间上的最值的方法,分类讨论的思想方法



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (2011•南通模拟)
(2011•南通模拟)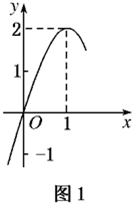 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.