
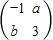 所对应的线性变换把直线l:2x-y=3变换为自身,求A-1.
所对应的线性变换把直线l:2x-y=3变换为自身,求A-1.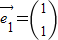 是矩阵B=
是矩阵B=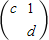 属于特征值λ1=2的一个特征向量,求矩阵B及其另一个特征值及其对应的一个特征向量.
属于特征值λ1=2的一个特征向量,求矩阵B及其另一个特征值及其对应的一个特征向量.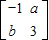 对应的变换把直线l:2x-y=3变换为自身,即直线l上的点经过变换后没有变,因此取直线l上的两点,对其进行变换列出方程方程组解出a、b得到矩阵M,最后根据逆矩阵的公式可求出A-1.
对应的变换把直线l:2x-y=3变换为自身,即直线l上的点经过变换后没有变,因此取直线l上的两点,对其进行变换列出方程方程组解出a、b得到矩阵M,最后根据逆矩阵的公式可求出A-1.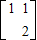 ,再回代到方程f(λ)=0即可解出另一个特征值为λ2=1,由此即可求出其对应的一个特征向量.
,再回代到方程f(λ)=0即可解出另一个特征值为λ2=1,由此即可求出其对应的一个特征向量. ,0),(0,-3).
,0),(0,-3).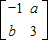 •
•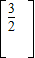 =
=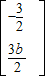 ,
,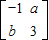 •
• =
=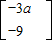 ,…(6分)
,…(6分) ,
, b),(-3a,-9)仍在直线l上.
b),(-3a,-9)仍在直线l上.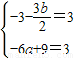 ,解之得
,解之得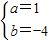
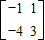 ,运用逆矩阵公式得
,运用逆矩阵公式得
 =
= …(10分)
…(10分)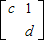 •
• =2
=2
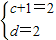 ,解之得c=1且d=2,得B=
,解之得c=1且d=2,得B=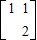
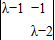 =0,解得矩阵B的另一个特征值λ2=1
=0,解得矩阵B的另一个特征值λ2=1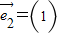 是属于特征值λ2=1的特征向量.
是属于特征值λ2=1的特征向量.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com