
分析 利用两个向量的加减法的法则,以及其几何意义,余弦定理,数形结合求得$\overrightarrow a$与$2\overrightarrow a-\overrightarrow b$夹角的余弦值.
解答 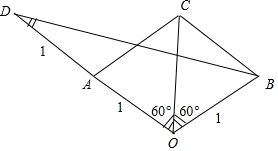 解:非零向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|$,不妨设$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|$=1,
解:非零向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|$,不妨设$|{\overrightarrow a}|=|{\overrightarrow b}|=|{\overrightarrow a+\overrightarrow b}|$=1,
设$\overrightarrow a$与$2\overrightarrow a-\overrightarrow b$夹角为θ,如图所示:
设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{a}$+$\overrightarrow{b}$,则OA=OB=OC=1,设$\overrightarrow{OD}$=2$\overrightarrow{OA}$=2$\overrightarrow{a}$,则$\overrightarrow{BD}$=2$\overrightarrow{a}$-$\overrightarrow{b}$,
∠ODB即为θ,△OAC和△OBC都是边长等于1的等边三角形.
利用余弦定理可得BD=$\sqrt{{OD}^{2}{+OB}^{2}-2OA•OB•cos120°}$=$\sqrt{7}$,
cosθ=$\frac{{OD}^{2}{+BD}^{2}{-OB}^{2}}{2OD•BD}$=$\frac{5\sqrt{7}}{14}$,
故答案为:$\frac{{5\sqrt{7}}}{14}$.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,余弦定理的应用,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={(\frac{1}{2})^x}$ | B. | y=-x2 | C. | y=log2x | D. | y=|x|+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 手机编号 | 1 | 2 | 3 | 4 | 5 |
| A型待机时间(h) | 120 | 125 | 122 | 124 | 124 |
| B型待机时间(h) | 118 | 123 | 127 | 120 | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com