
分析 (Ⅰ)设过点P(0,2)的直线l:y=kx+2,联立直线与抛物线方程,令A(x1,y1),B(x2,y2),利用韦达定理,求解$\overrightarrow{OA}•\overrightarrow{OB}$为定值.
(Ⅱ)由(Ⅰ)知,利用弦长公式以及原点到直线l的距离$d=\frac{2}{{\sqrt{1+{k^2}}}}$,表示三角形的面积,然后求解最小值即可.
解答 证明:(Ⅰ)设过点P(0,2)的直线l:y=kx+2,
由$\left\{{\begin{array}{l}{y=kx+2}\\{y=4{x^2}}\end{array}}\right.$得,4x2-kx-2=0,
令A(x1,y1),B(x2,y2),∴${x_1}+{x_2}=\frac{k}{4},{x_1}{x_2}=-\frac{1}{2}$,y1y2=k2x1x2+2k(x1+x2)+4=4
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=4-$\frac{1}{2}$=$\frac{7}{2}$为定值.------(6分)
解:(Ⅱ)由(Ⅰ)知,$|AB|=|{x_1}-{x_2}|\sqrt{1+{k^2}}=\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}\sqrt{1+{k^2}}$=$\frac{1}{4}\sqrt{{k^2}+1}\sqrt{32+{k^2}}$,
原点到直线l的距离$d=\frac{2}{{\sqrt{1+{k^2}}}}$
∴${S_{△AOB}}=\frac{1}{2}×|AB|×d=4\sqrt{{k^2}+2}≥\sqrt{2}$
当k=0时,三角形AOB的面积最小,最小值是$\sqrt{2}$------(12分)
点评 本题考查抛物线的简单性质的应用,直线与抛物线的位置关系,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
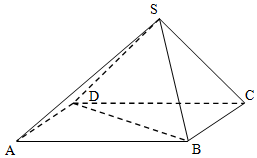 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
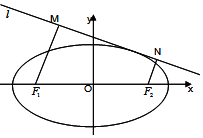 已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.
已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
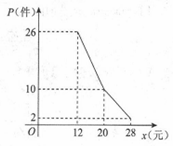 某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com