
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)求证:当![]() 时,
时,![]() ;
;
(Ⅱ)若存在![]() ,使
,使![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)所证明不等式转化为![]() ,设
,设![]() , 利用导数判断函数的单调性,并利用最值证明;
, 利用导数判断函数的单调性,并利用最值证明;
(Ⅱ)首先判断函数![]() 的单调性,再分
的单调性,再分![]() 和
和![]() 两种情况求
两种情况求![]() 的取值范围,当
的取值范围,当![]() 时,
时,![]() 成立,求
成立,求![]() ,当
,当![]() 时,根据(1)的结论证明
时,根据(1)的结论证明![]() 时,
时,![]() ,当
,当![]() 时,设
时,设![]() ,利用导数证明
,利用导数证明![]() ,综上证明过程求
,综上证明过程求![]() 的取值范围.
的取值范围.
解:(Ⅰ)解:![]() 的定义域为
的定义域为![]() ,
,
![]() ,即
,即![]()
设![]() ,
,
![]() ,故
,故![]() 在
在![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,得证.
,得证.
(Ⅱ)![]() ,故
,故![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,
,
对于![]() ,
,
(1)当![]() 时,
时,![]() ,需要
,需要![]() ,
,![]() ;
;
(2)当![]() 时,先证若
时,先证若![]() ,有
,有![]() ,
,
(ⅰ)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
![]()
![]() 是减函数,
是减函数,![]() ,
,
![]() ,
,![]()
(ⅱ)若![]() ,设
,设![]() ,
,
![]() 是增函数,
是增函数,![]() ,
,![]() ,
,
故有![]() ,使
,使![]() ,
,![]() 在
在![]() 减,在
减,在![]() 增,
增,
![]() ,
,![]() ,
,
![]() 时,
时,![]() ,得
,得![]()
由(ⅰ)(ⅱ)得,当![]() 时,
时,![]()
此时由于![]() ,
,![]() 时,
时,![]() ,故
,故![]() ,满足题意.
,满足题意.
综上可得,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某房地产商建有三栋楼宇![]() ,三楼宇间的距离都为2千米,拟准备在此三楼宇围成的区域
,三楼宇间的距离都为2千米,拟准备在此三楼宇围成的区域![]() 外建第四栋楼宇
外建第四栋楼宇![]() ,规划要求楼宇
,规划要求楼宇![]() 对楼宇
对楼宇![]() ,
,![]() 的视角为
的视角为![]() ,如图所示,假设楼宇大小高度忽略不计.
,如图所示,假设楼宇大小高度忽略不计.
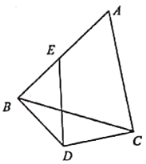
(1)求四栋楼宇围成的四边形区域![]() 面积的最大值;
面积的最大值;
(2)当楼宇![]() 与楼宇
与楼宇![]() ,
,![]() 间距离相等时,拟在楼宇
间距离相等时,拟在楼宇![]() ,
,![]() 间建休息亭
间建休息亭![]() ,在休息亭
,在休息亭![]() 和楼宇
和楼宇![]() ,
,![]() 间分别铺设鹅卵石路
间分别铺设鹅卵石路![]() 和防腐木路
和防腐木路![]() ,如图,已知铺设鹅卵石路、防腐木路的单价分别为
,如图,已知铺设鹅卵石路、防腐木路的单价分别为![]() ,
,![]() (单位:元千米,
(单位:元千米,![]() 为常数).记
为常数).记![]() ,求铺设此鹅卵石路和防腐木路的总费用的最小值.
,求铺设此鹅卵石路和防腐木路的总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
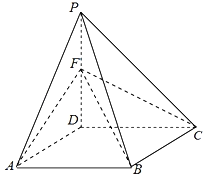
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列正确的是( )
,下列正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点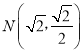 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com