
【题目】求下列不等式的解集:
(1)![]()
(2)![]()
(3)![]()
(4)![]()
【答案】(1)![]() ;(2)
;(2)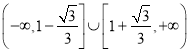 ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据一元二次不等式的解法,求得不等式的解集.
(2)根据一元二次不等式的解法,求得不等式的解集.
(3)根据一元二次不等式的解法,求得不等式的解集.
(4)根据一元二次不等式的解法,求得不等式的解集.
(1)方法一(因式分解法)因为![]() ,
,
所以原不等式可化为![]() ,解得
,解得![]() ,
,
所以原不等式的解集为![]() .
.
方法二(配方法)原不等式化为![]() ,因为
,因为![]() ,
,
所以原不等式可化为![]() ,即
,即![]() ,
,
两边开平方,得![]() ,即
,即![]() ,所以
,所以![]() .
.
所以原不等式的解集为![]() .
.
(2)原不等式化为![]() ,因为
,因为![]() ,
,
所以原不等式可化为![]() ,即
,即![]() .两边开平方,得
.两边开平方,得![]() ,
,
即![]() 或
或![]() .所以
.所以![]() 或
或![]() ,
,
所以原不等式的解集为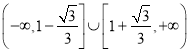 .
.
(3)原不等式可化为![]() ,所以原不等式的解集为
,所以原不等式的解集为![]() .
.
(4)原不等式可化为![]() ,即
,即![]() ,即
,即![]() ,所以原不等式的解集为
,所以原不等式的解集为![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,点D在棱
,点D在棱![]() 上,且
上,且![]() ,建立如图所示的空间直角坐标系.
,建立如图所示的空间直角坐标系.

(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 的夹角的余弦值;
的夹角的余弦值;
(2)若二面角![]() 的平面角为
的平面角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某电子元件进行寿命追踪调查,情况如下:
寿命分组/h | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个数 | 20 | 30 | 80 | 40 | 30 |
(1)求下表中的x,y;
寿命分组/h | 频数 | 频率 |
100~200 | 20 | 0.10 |
200~300 | 30 | x |
300~400 | 80 | 0.40 |
400~500 | 40 | 0.20 |
500~600 | 30 | y |
合计 | 200 | 1 |
(2)从频率分布直方图估计电子元件寿命的第80百分位数是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的单调增区间;最大值,以及取得最大值时x的取值集合;
的单调增区间;最大值,以及取得最大值时x的取值集合;
(2)已知![]() 中,角A、B、C的对边分别为a,b,c,若
中,角A、B、C的对边分别为a,b,c,若![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
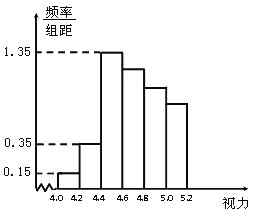

(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据
![]()
(1)利用所给数据求年需求量与年份之间的回归直线方程![]() ;
;
(2)利用(1)计算2002年和2006年粮食需求量的残差;
(3)利用(1)中所求出的直线方程预测该地2012年的粮食需求量。
公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁![]() 59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列2×2列联表,并回答能否有90%的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2 人能胜任的2人能胜任才艺表演的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】火电厂、核电站的循环水自然通风冷却塔是一种大型薄壳型构筑物。建在水源不十分充足的地区的电厂,为了节约用水,需建造一个循环冷却水系统,以使得冷却器中排出的热水在其中冷却后可重复使用,大型电厂采用的冷却构筑物多为双曲线型冷却塔.此类冷却塔多用于内陆缺水电站,其高度一般为75~150米,底边直径65~120米. 双曲线型冷却塔比水池式冷却构筑物占地面积小,布置紧凑,水量损失小,且冷却效果不受风力影响;它比机力通风冷却塔维护简便,节约电能;但体形高大,施工复杂,造价较高.(以上知识来自百度,下面题设条件只是为了适合高中知识水平,其中不符合实际处请忽略.)

(1)如图为一座高100米的双曲线冷却塔外壳的简化三视图(忽略壁厚),其底面直径大于上底直径,已知其外壳主视图与左视图中的曲线均为双曲线,高度为100![]() ,俯视图为三个同心圆,其半径分别40
,俯视图为三个同心圆,其半径分别40![]() ,
,![]()
![]() ,30
,30![]() ,试根据上述尺寸计算视图中该双曲线的标准方程(
,试根据上述尺寸计算视图中该双曲线的标准方程(![]() 为长度单位米);
为长度单位米);

(2)试利用课本中推导球体积的方法,利用圆柱和一个倒放的圆锥,计算封闭曲线:![]() ,
,![]() ,绕
,绕![]() 轴旋转形成的旋转体的体积多少?(用
轴旋转形成的旋转体的体积多少?(用![]() 表示).(用积分计算不得分)现已知双曲线冷却塔是一个薄壳结构,为计算方便设其内壁所在曲线也为双曲线,其壁最厚为0.4
表示).(用积分计算不得分)现已知双曲线冷却塔是一个薄壳结构,为计算方便设其内壁所在曲线也为双曲线,其壁最厚为0.4![]() (底部),最薄处厚度为0.3
(底部),最薄处厚度为0.3![]() (喉部,即左右顶点处),试计算该冷却塔内壳所在的双曲线标准方程是?并计算本题中的双曲线冷却塔的建筑体积(内外壳之间)大约是多少
(喉部,即左右顶点处),试计算该冷却塔内壳所在的双曲线标准方程是?并计算本题中的双曲线冷却塔的建筑体积(内外壳之间)大约是多少![]() ;(计算时
;(计算时![]() 取3.14159,保留到个位即可)
取3.14159,保留到个位即可)

(3)冷却塔体型巨大,造价相应高昂,本题只考虑地面以上部分的施工费用(建筑人工和辅助机械)的计算,钢筋土石等建筑材料费用和和其它设备等施工费用不在本题计算范围内.超高建筑的施工(含人工辅助机械等)费用随着高度的增加而增加,现已知:距离地面高度30米(含30米)内的建筑,每立方米的施工费用平均为:400元/立方米;30米到40米(含40米)每立方米的施工费用为800元/立方米;40米以上,平均高度每增加1米,每立方米的施工费用增加100元.试计算建造本题中冷却塔的施工费用(精确到万元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com