
【题目】已知函数 ![]() (
( ![]() )
)
(1)若曲线 ![]() 在点
在点 ![]() 处的切线经过点
处的切线经过点 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() 在
在 ![]() 内存在极值,求
内存在极值,求 ![]() 的取值范围;
的取值范围;
(3)当 ![]() 时,
时, ![]() 恒成立,求
恒成立,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解: ![]() .
.
![]() ,
, ![]() .
.
因为 ![]() 在
在 ![]() 处的切线过
处的切线过 ![]() ,所以
,所以 ![]() .
.
(2)解: ![]() 在
在 ![]() 内有解且
内有解且 ![]() 在
在 ![]() 内有正有负.
内有正有负.
令 ![]() .
.
由 ![]() ,得
,得 ![]() 在
在 ![]() 内单调递减,
内单调递减,
所以 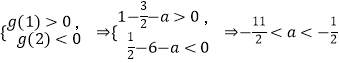 .
.
(3)解:因为 ![]() 时
时 ![]() 恒成立,所以
恒成立,所以 ![]() .
.
令 ![]() ,则
,则 ![]() .
.
令 ![]() ,由
,由 ![]() ,得
,得 ![]() 在
在 ![]() 内单调递减,又
内单调递减,又 ![]() ,
,
所以 ![]() 时
时 ![]() ,即
,即 ![]() ,
, ![]() 单调递增,
单调递增, ![]() 时
时 ![]() ,
,
即 ![]() ,
, ![]() 单调递减.所以
单调递减.所以 ![]() 在
在 ![]() 内单调递增,
内单调递增,
在 ![]() 内单调递减,所以
内单调递减,所以 ![]() .所以
.所以 ![]() .
.
【解析】(1)考察了曲线切线的斜率与导数的关系
(2)考察了极值与导数的关系,以及函数零点的存在性定理;f ( x ) 在 ( 1 , 2 ) 内存在极值,等价于 f ′ ( x ) = 0 在 ( 1 , 2 ) 内有解且f ′ ( x )在 ( 1 , 2 ) 内有正有负,及结合f ′ ( x )的导函数,判断f ′ ( x )是单调减函数,因此运用函数零点存在性定理,只要g(1)>0 ,g(2)<0即可;
(3)考察函数含参恒成立问题的一般解法,分离参数法,进而利用函数单调性求最值。
注意第三问是证明恒成立问题,首先分离参数,可得a >![]() ,构造函数 h ( x ) =
,构造函数 h ( x ) = ![]() ,只要a大于h(x)得最大值,再利用导数确定h(x)的单调性,注意一次求导不可得,再求一次,即可确定h(x)得单调性,即可
,只要a大于h(x)得最大值,再利用导数确定h(x)的单调性,注意一次求导不可得,再求一次,即可确定h(x)得单调性,即可
【考点精析】解答此题的关键在于理解导数的几何意义的相关知识,掌握通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ,以及对函数的极值与导数的理解,了解求函数
,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】
已知等差数列![]() ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 仍为数列
仍为数列![]() 中的项,若存在,求出所有满足的正整数
中的项,若存在,求出所有满足的正整数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·上海)设z1, z2![]() C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
C, ,则“z1, z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2﹣4x﹣5=0”的充分不必要条件
C.命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x≥﹣1,则x2﹣2x﹣3≤0”
D.已知命题 p:x∈R,x2+x﹣1<0,则p:x∈R,x2+x﹣1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》有如下问题:有上禾三秉(古代容量单位),中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉,实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾一秉各几何?依上文:设上、中、下禾一秉分别为x斗、y斗、z斗,设计如图所示的程序框图,则输出的x,y,z的值分别为( ) 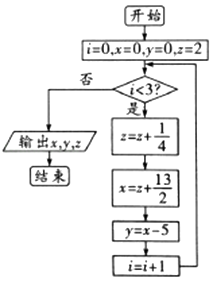
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com