Question

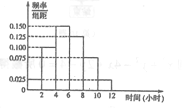
【题目】我校高二年级共2000名学生，其中男生1200人.为调查学生们的手机使用情况，采用分层抽样的方法，随机抽取100位学生每周平均使用手机上网时间的样本数据（单位：小时）.根据这100个数据，得到学生每周平均使用手机上网时间的频率分布直方图（如图所示），其中样本数据分组区间分别为.

（1）应收集男生、女生样本数据各多少人？

（2）估计我校高二年级学生每周平均使用手机上网时间超过4小时的概率.

（3）将平均每周使用手机上网时间在内定义为“长时间使用手机”，在内定义为“短时间使用手机”.在样本数据中，有25名学生不近视.请完成下列2×2列联表，并判断是否有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.

	近视	不近视	合计
长时间使用手机上网
短时间使用手机上网		15
合计		25

附：

	0.100	0.050	0.010	0.005
	2.706	3.841	6.635	7.879

Answer 1

【答案】(1)60人，40人，(2)0.75(3) 有99.5%的把握认为“学生每周使用手机上网时间与近视程度有关”.

【解析】分析：（1）高二年级男女生之比为，故按比例抽取的男生人数为，女生人数为.

（2）用样本中的频率代替概率，计算上网时间小于4的频率（也就是概率）可得上网时间不少于4小时的概率.

（3）根据（2）的概率得到百人中长时间上网的人数为，从而可得表中缺省的各数据.通过计算的值来判断使用手机上网时间与近视的相关程度.

详解：（1）男生人数：（人），女生人数：（人）；

（2）学生每周平均使用手机上网时间超过4小时的概率

；

（3）由（2）问可知，的人数为75人，的人数为25人.则2×2列联表如下：

	近视	不近视	合计
长时间使用手机上网	65	10	75
短时间使用手机上网	10	15	25
合计	75	25	100

，

故有的把握认为“学生每周使用手机上网时间与近视程度有关”.