
【题目】如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小.
(2)求DP与平面AA′D′D所成角的大小.
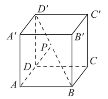
【答案】(1)45°.(2)30°.
【解析】
(1)以D为原点,DA,DC,DD′分别为x轴,y轴,z轴正方向建立空间直角坐标系,连接BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H. 设![]() =(m,m,1)(m>0), 由<
=(m,m,1)(m>0), 由<![]() ,
,![]() >=60°,利用坐标运算可得m,进而可得cos<
>=60°,利用坐标运算可得m,进而可得cos<![]() ,
,![]() >,从而得解;
>,从而得解;
(2)平面AA′D′D的一个法向量是![]() =(0,1,0),由cos<
=(0,1,0),由cos<![]() ,
,![]() >即可得解.
>即可得解.
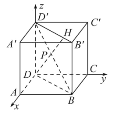
(1)如图所示,以D为原点,DA,DC,DD′分别为x轴,y轴,z轴正方向建立空间直角坐标系,
设DA=1.则![]() =(1,0,0),
=(1,0,0),![]() =(0,0,1).连接BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.
=(0,0,1).连接BD,B′D′.在平面BB′D′D中,延长DP交B′D′于H.
设![]() =(m,m,1)(m>0),
=(m,m,1)(m>0),
由已知<![]() ,
,![]() >=60°,由
>=60°,由![]() ·
·![]() =|
=|![]() ||
||![]() |cos<
|cos<![]() ,
,![]() >,可得2m=
>,可得2m=![]() .解得m=
.解得m=![]() ,
,
所以![]() =
=![]() .
.
因为cos<![]() ,
,![]() >=
>=![]() =
=![]()
所以<![]() ,
,![]() >=45°,即DP与CC′所成的角为45°.
>=45°,即DP与CC′所成的角为45°.
(2)平面AA′D′D的一个法向量是![]() =(0,1,0),
=(0,1,0),
因为cos<![]() ,
,![]() >=
>=![]() =
=![]()
所以<![]() ,
,![]() >=60°,可得DP与平面AA′D′D所成的角为30°.
>=60°,可得DP与平面AA′D′D所成的角为30°.


科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,它的前
,它的前![]() 项和为
项和为![]() ,
,
(ⅰ)求![]() ;
;
(ⅱ)若存在正整数![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不共线的向量![]() ,
,![]() 夹角为
夹角为![]() ,且
,且![]() ,
,![]() ,为正实数.
,为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值及对应的x的值,并指出此时向量
的最小值及对应的x的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数m,关于x的方程
为锐角,对于正实数m,关于x的方程![]() 两个不同的正实数解,且
两个不同的正实数解,且![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
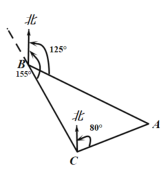
【题目】如图,货轮在海上B处,以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行,为了确定船位,在B点处观测到灯塔A的方位角为125o.半小时后,货轮到达C点处,观测到灯塔A的方位角为80o.求此时货轮与灯塔之间的距离(答案保留最简根号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A.已知直线![]() 和平面
和平面![]() ,若点
,若点![]() ,点
,点![]() 且
且![]() ,
,![]() ,则
,则![]()
B.若三条直线两两相交,则三条直线确定一个平面
C.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则
,则![]() 内的所有直线与
内的所有直线与![]() 都不相交
都不相交
D.若直线![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,则l至少与
,则l至少与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率是40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定l,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下10组随机数:907 966 191 925 271 431 932 458 569 683.
据此估计,该运动员三次投篮恰有两次命中的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com