
【题目】已知在锐角△ABC中,两向量p=(2-2sin A,cos A+sin A),q=(sin A-cos A,1+sin A),且p与q是共线向量.
(1)求A的大小;
(2)求函数y=2sin2B+cos(![]() )取最大值时,角B的大小.
)取最大值时,角B的大小.
【答案】(1)A=60°(2)B=60°
【解析】试题分析:
(1)利用向量平行的充要条件求得![]() ,结合锐角三角形可得A=60°;
,结合锐角三角形可得A=60°;
(2)整理函数的解析式可得y=1+sin(2B-30°)结合角的范围可得B=60°时,函数取最大值2.
试题解析:
解:(1)∵p∥q,
∴(2-2sin A)(1+sin A)-(cos A+sin A)(sin A-cos A)=0
∴sin2A=![]() ,sin A=
,sin A=![]()
∵△ABC为锐角三角形,∴A=60°.
(2)y=2sin2B+cos(![]() )=2sin2B+cos(
)=2sin2B+cos(![]() )
)
=2sin2B+cos(2B-60°)=1-cos 2B+cos(2B-60°)
=1-cos 2B+cos 2Bcos 60°+sin 2Bsin 60°
=1-![]() cos 2B+
cos 2B+![]() sin 2B=1+sin(2B-30°)
sin 2B=1+sin(2B-30°)
当2B-30°=90°,即B=60°时,函数取最大值2.


科目:高中数学 来源: 题型:
【题目】袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,X表示所取球的标号.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某动物园要建造两间完全相同的矩形熊猫居室,其总面积为24平方米,设熊猫居室的一面墙![]() 长为
长为![]() 米(2
米(2![]() ).
).
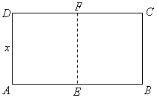
⑴用![]() 表示墙
表示墙![]() 的长;
的长;
⑵假设所建熊猫居室的墙壁造价(在墙壁高度一定的前提下)为每米1000元,请将墙壁的总造价![]() (元)表示为
(元)表示为![]() (米)的函数;
(米)的函数;
⑶当![]() 为何值时,墙壁的总造价最低?
为何值时,墙壁的总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(必须列式,不能只写答案,答案用数字表示)有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)求共有多少种放法;
(2)求恰有一个盒子不放球,有多少种放法;
(3)求恰有两个盒内不放球,有多少种放法;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com