
分析 由$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,知g(x)=xf(x)在(-∞,0)上单调递减,由f(x)的奇偶性可判断g(x)的奇偶性及特殊点,从而可作出草图,由图象可解g(3x)<0,进而得到答案.
解答 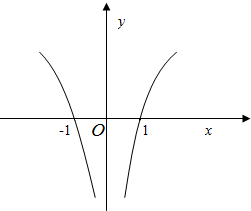 解:∵$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
解:∵$\frac{{x}_{1}f({x}_{1})-{x}_{2}f({x}_{2})}{{x}_{1}-{x}_{2}}$<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
∴函数g(x)=xf(x)在(-∞,0)上单调递减,
又 f(x)为奇函数,∴g(x)=xf(x)为偶函数,
g(x)在(0,+∞)上单调递增,且g(-1)=g(1)=0,
作出g(x)的草图如图所示:
2xf(3x)<0即g(3x)<0,
由图象得,-1<3x<0或0<3x<1,解得-$\frac{1}{3}$<x<0或0<x<$\frac{1}{3}$,
∴不等式2xf(3x)<0解集是(-$\frac{1}{3}$,0)∪(0,$\frac{1}{3}$),
故答案为:(-$\frac{1}{3}$,0)∪(0,$\frac{1}{3}$).
点评 本题考查函数的奇偶性、单调性及其应用,考查不等式的求解,综合运用函数性质化抽象不等式为具体不等式是解题关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com