练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校高三年级举行了一次全年级的大型考试,在数学成绩优秀和非优秀的学生中,物理、化学、总分成绩也为优秀的人数如下表所示,则我们能以99%的把握认为数学成绩优秀与物理、化学、总分成绩优秀有关系吗?

    物理优秀

    化学优秀

    总分优秀

    数学优秀

    228

    225

    267

    数学非优秀

    143

    156

    99

    注:该年级此次考试中数学成绩优秀的有360人,非优秀的有880人.

    【答案】见解析

    【解析】分析：利用独立性检验分别计算，再判断我们是否能以99%的把握认为数学成绩优秀与物理、化学、总分成绩优秀有关系.

    详解：(1)根据已知数据列出数学与物理成绩的2×2列联表如下表所示:

    物理优秀

    物理非优秀

    合计

    数学优秀

    228

    b

    360

    数学非优秀

    143

    d

    880

    合计

    371

    b+d

    1 240

    则b=360-228=132,d=880-143=737,b+d=132+737=869.代入公式可得

    270.114.

    (2)按照上述方法列出数学与化学成绩的2×2列联表如下表所示:

    化学优秀

    化学非优秀

    合计

    数学优秀

    225

    135

    360

    数学非优秀

    156

    724

    880

    合计

    381

    859

    1 240

    代入公式可得

    240.611.

    (3)列出数学与总分成绩的2×2列联表如下表所示:

    总分优秀

    总分非优秀

    合计

    数学优秀

    267

    93

    360

    数学非优秀

    99

    781

    880

    合计

    366

    874

    1 240

    代入公式可得486.123.

    由于计算出的χ2的观测值都大于6.635,因此说明有99%的把握认为数学成绩优秀与物理、化学、总分成绩优秀有关系.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C1： +y2=1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．
    （1）求椭圆C2的方程；
    （2）设O为坐标原点，点A，B分别在椭圆C1和C2上， =2 ，求直线AB的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭10次，命中的环数如下：

    甲

    8

    9

    7

    9

    7

    6

    10

    10

    8

    6

    乙

    10

    9

    8

    6

    8

    7

    9

    7

    8

    8

    (1)计算甲、乙两人射箭命中环数的平均数和标准差；

    (2)比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

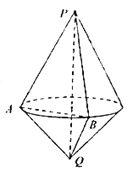
    【题目】下图中的几何体是由两个有共同底面的圆锥组成．已知两个圆锥的顶点分别为P、Q，高分别为2、1，底面半径为1．A为底面圆周上的定点，B为底面圆周上的动点（不与A重合）．下列四个结论：

    ①三棱锥体积的最大值为；

    ②直线PB与平面PAQ所成角的最大值为；

    ③当直线BQ与AP所成角最小时，其正弦值为；

    ④直线BQ与AP所成角的最大值为；

    其中正确的结论有___________.（写出所有正确结论的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三棱柱ABC﹣A1B1C1中，底面边长和侧棱长都相等，∠BAA1=∠CAA1=60°，则异面直线AB1与BC1所成角的余弦值为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，定义域为上的函数是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.

    （1）求的解析式；

    （2）若关于的方程有三个不同解，求的取值范围；

    （3）若，求的取值集合.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（12分）已知函数f（x）=

    （1）判断函数在区间[1,+∞）上的单调性,并用定义证明你的结论．

    （2）求该函数在区间[1,4]上的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数. 为实数，且，记由所有组成的数集为.

    （1）已知，求；

    （2）对任意的，恒成立，求的取值范围；

    （3）若，，判断数集中是否存在最大的项？若存在，求出最大项；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三点O（0，0），A（﹣2，1），B（2，1），曲线C上任意一点M（x，y）满足| + |= （ + ）+2．
    （1）求曲线C的方程；
    （2）动点Q（x0 ， y0）（﹣2＜x0＜2）在曲线C上，曲线C在点Q处的切线为直线l：是否存在定点P（0，t）（t＜0），使得l与PA，PB都相交，交点分别为D，E，且△QAB与△PDE的面积之比是常数？若存在，求t的值．若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案