
【题目】命题p:![]() x∈R,ax2﹣2ax+1>0,命题q:指数函数f(x)=ax(a>0且a≠1)为减函数,则P是q的( )
x∈R,ax2﹣2ax+1>0,命题q:指数函数f(x)=ax(a>0且a≠1)为减函数,则P是q的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
科目:高中数学 来源: 题型:
【题目】(多选题)有下列几个命题,其中正确的命题是( )
A.函数![]() 在
在![]() 上是增函数
上是增函数
B.函数![]() 在
在![]() 上是减函数
上是减函数
C.函数![]() 的单调区间是
的单调区间是![]()
D.已知![]() 在
在![]() 上是增函数,若
上是增函数,若![]() ,则有
,则有![]()
E.已知函数 是奇函数,则
是奇函数,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将标号为1,2,…,20的20张卡片放入下列表格中,一个格放入一张卡片,选出每列标号最小的卡片,将这些卡片中标号最大的数设为![]() ;选出每行标号最大的卡片,将这些卡片中标号最小的数设为
;选出每行标号最大的卡片,将这些卡片中标号最小的数设为![]() .
.
甲同学认为![]() 有可能比
有可能比![]() 大,乙同学认为
大,乙同学认为![]() 和
和![]() 有可能相等,那么甲乙两位同学的说法中( )
有可能相等,那么甲乙两位同学的说法中( )
A. 甲对乙不对 B. 乙对甲不对 C. 甲乙都对 D. 甲乙都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的一种电器的固定成本(即固定投资)为0.5万元,每生产一台这种电器还需可变成本(即另增加投资)25元,市场对这种电器的年需求量为5百台.已知这种电器的销售收入R与销售量t的关系可用抛物线表示,如图.
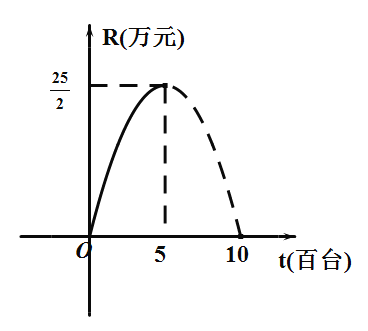
(注:销售量的单位:百台,销售收入与纯收益的单位:万元,生产成本=固定成本+可变成本,精确到1台和0.01万元)
(1)写出销售收入R与销售量t之间的函数关系式;
(2)若销售收入减去生产成本为纯收益,写出纯收益与销售量的函数关系式,并求销售量是多少时,纯收益最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假.
(1)如果直线![]() 平行于直线
平行于直线![]() ,则
,则![]() 平行于经过
平行于经过![]() 的任何一个平面;
的任何一个平面;
(2)如果一条直线不在平面内,则这条直线就与这个平面平行;
(3)过直线外一点,可以作无数个平面与这条直线平行;
(4)如果一条直线与一个平面平行,则它与该平面内的任何直线都平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校共有学生15000人,其中男生10500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4小时的概率.

(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.

附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,则下列关于
的图象,则下列关于![]() 的说法正确的是( )
的说法正确的是( )
A.最大值为1,图象关于直线![]() 对称
对称
B.周期为![]() ,图象关于点
,图象关于点![]() 对称
对称
C.图象关于y轴对称,在![]() 上单调递减
上单调递减
D.在![]() 上单调递增,且为偶函数
上单调递增,且为偶函数
E.在![]() 上单调递减,且为奇函数
上单调递减,且为奇函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com