
【题目】已知动圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x﹣4)2+y2=2内切,求动圆圆心M的轨迹方程. 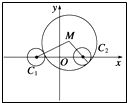
【答案】解:设动圆圆心M(x,y),半径为r,∵圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x﹣4)2+y2=2内切,
∴|MC1|=r+ ![]() ,|MC2|=r﹣
,|MC2|=r﹣ ![]() ,
,
∴|MC1|﹣|MC2|=2 ![]() <8,
<8,
由双曲线的定义,可得a= ![]() ,c=4;则b2=c2﹣a2=14;
,c=4;则b2=c2﹣a2=14;
∴点M的轨迹是以点C1 , C2为焦点的双曲线的一支,
∴动圆圆心M的轨迹方程: ![]() ﹣
﹣ ![]()
【解析】根据两圆外切和内切的判定,圆心距与两圆半径和差的关系,设出动圆半径为r,消去r,根据圆锥曲线的定义,即可求得动圆圆心M的轨迹,进而可求其方程.
【考点精析】通过灵活运用双曲线的概念,掌握平面内与两个定点![]() ,
,![]() 的距离之差的绝对值等于常数(小于
的距离之差的绝对值等于常数(小于![]() )的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距即可以解答此题.
)的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距即可以解答此题.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=4cosθ.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直l的参数方程是![]() (t是参数)
(t是参数)
(1)将曲线C的极坐标方程化为直角坐标方程;
(2)若直线l与曲线C相交于A、B两点,且|AB|=![]() ,求直线的倾斜角α的值.
,求直线的倾斜角α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cosx,C2:y=sin(2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角ABC中,角A、B、C所对的边分别为a,b,c,b=4,c=6,且asinB=2![]() .
.
(1)求角A的大小;
(2)若D为BC的中点,求线段AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C的对边分别为a,b,c,且a,b,c成等比数列
(1)若sinC=2sinA,求cosB的值;
(2)求角B的最大值.并判断此时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点A,B,C,D在同一个球的球面上,AB=BC=2,AC=2 ![]() ,若四面体ABCD体积的最大值为
,若四面体ABCD体积的最大值为 ![]() ,则该球的表面积为( )
,则该球的表面积为( )
A.![]()
B.8π
C.9π
D.12π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题:粮仓开仓收粮,粮农送来米1512石,验得米内夹谷,抽样取米一把,数得216粒内夹谷27粒,则这批米内夹谷约( )
A.164石
B.178石
C.189石
D.196石
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com