
【题目】设函数f(x)=sin(2x+ ![]() )+
)+ ![]() cos(2x+
cos(2x+ ![]() ),则( )
),则( )
A.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
B.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
C.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
D.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
科目:高中数学 来源: 题型:
【题目】在公差不为零的等差数列{an}和等比数列{bn}中.已知a1=b1=1.a2=b2 . a6=b3
(1)求等差数列{an}的通项公式an和等比数列{bn}的通项公式bn;
(2)求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式组 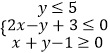 表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
A.[10,+∞)
B.[11,+∞)
C.[13,+∞)
D.[14,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且a2+c2=b2﹣ac.
(1)求B的大小;
(2)设∠BAC的平分线AD交BC于D,AD=2 ![]() ,BD=1,求cosC的值.
,BD=1,求cosC的值. 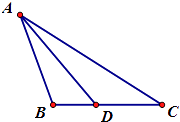
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两煤矿每年的产量分别为200万吨和260万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站毎年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/t和1.5元/t,乙煤矿运往东车站和西车站的运费价格分别为0.8元/t和1.6元/t.煤矿应怎样编制调运方案,能使总运费最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王为了锻炼身体,每天坚持“健步走”,并用计步器进行统计.小王最近8天“健步走”步数的频数分布直方图(图1)及相应的消耗能量数据表(表1)如下:
健步走步数(前步) | 16 | 17 | 18 | 19 |
消耗能量(卡路里) | 400 | 440 | 480 | 520 |
(Ⅰ)求小王这8天“健步走”步数的平均数;
(Ⅱ)从步数为17千步,18千步,19千步的几天中任选2天,求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率.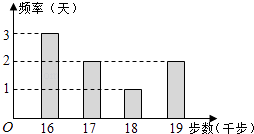
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题: ①“若a2<b2 , 则a<b”的否命题;
②“全等三角形面积相等”的逆命题;
③“若a>1,则ax2﹣2ax+a+3>0的解集为R”的逆否命题;
④“若 ![]() x(x≠0)为有理数,则x为无理数”的逆否命题.
x(x≠0)为有理数,则x为无理数”的逆否命题.
其中正确的命题是( )
A.③④
B.①③
C.①②
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点O是平面上一定点,A、B、C是平面上△ABC的三个顶点,∠B、∠C分别是边AC、AB的对角,以下命题正确的是(把你认为正确的序号全部写上). ①动点P满足 ![]() =
= ![]() +
+ ![]() +
+ ![]() ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中;
②动点P满足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),则△ABC的内心一定在满足条件的P点集合中;
)(λ>0),则△ABC的内心一定在满足条件的P点集合中;
③动点P满足 ![]() =
= ![]() +λ(
+λ( 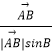 +
+ 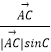 )(λ>0),则△ABC的重心一定在满足条件的P点集合中;
)(λ>0),则△ABC的重心一定在满足条件的P点集合中;
④动点P满足 ![]() =
= ![]() +λ(
+λ( 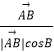 +
+ 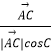 )(λ>0),则△ABC的垂心一定在满足条件的P点集合中;
)(λ>0),则△ABC的垂心一定在满足条件的P点集合中;
⑤动点P满足 ![]() =
= ![]() +λ(
+λ( 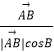 +
+ 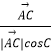 )(λ>0),则△ABC的外心一定在满足条件的P点集合中.
)(λ>0),则△ABC的外心一定在满足条件的P点集合中.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 已知S2=4,an+1=2Sn+1,n∈N* .
(1)求通项公式an;
(2)求数列{|an﹣n﹣2|}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com