解:(1)∵设平面向量

满足
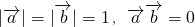
,
又∵
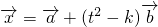
,
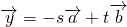
,
当
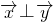
时,
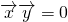
即[

]•[

]=0
即-S+t
3-kt=0
故s=t
3-kt…(4分)
(2)∵k=3,
∴s=t
3-3t,s'=3t
2-3,
由s'=0?t
1=-1,t
2=1,
f(t)在(-∞,-1)上递增,(-1,1)上递减,(1,+∞)递增,
又∵f(-1)=2,f(3)=18,
∴s的最大值为18 …(10分)
(3)∵
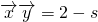
,
∴-s+t
3-kt=2-s,t
3-2=kt,…(12分)
当t=0时,等式不成立;
当t≠0时,

k(t)在(-∞,-1)上递减,(-1,0)上递增,(0,+∞)递增,
结合图象可知k<3时符合要求.…(16分)
分析:(1)由已知中平面向量

满足
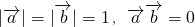
,
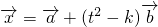
,
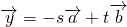
,若
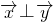
,则
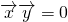
,代入整理可得函数关系式s=f(t);
(2)令k=3,可得s=t
3-3t,则s'=3t
2-3,分析函数的单调性可得t∈[-2,3]时,s的最大值.
(3))由已知可得
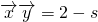
,故-s+t
3-kt=2-s,t
3-2=kt,分别分析当t=0时和当t≠0时,等式成立的条件,可得结论.
点评:本题考查的知识点是平面向量的数量积运算,导数法判断函数的单调性,导数法求函数在定区间上的最值,其中根据平面向量的数量积运算公式,求出s关于变量t函数的解析式,是解答本题的关键.

 满足
满足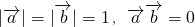 ,
,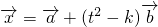 ,
,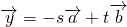 ,其中,k,t,s∈R.
,其中,k,t,s∈R.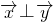 ,求函数关系式s=f(t);
,求函数关系式s=f(t);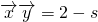 .
. 满足
满足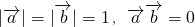 ,
,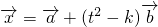 ,
,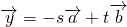 ,
,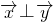 时,
时,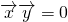
 ]•[
]•[ ]=0
]=0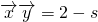 ,
,
 满足
满足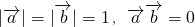 ,
,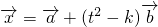 ,
,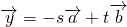 ,若
,若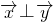 ,则
,则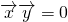 ,代入整理可得函数关系式s=f(t);
,代入整理可得函数关系式s=f(t);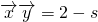 ,故-s+t3-kt=2-s,t3-2=kt,分别分析当t=0时和当t≠0时,等式成立的条件,可得结论.
,故-s+t3-kt=2-s,t3-2=kt,分别分析当t=0时和当t≠0时,等式成立的条件,可得结论.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案 满足
满足 ,
, ,
, ,其中,k,t,s∈R.
,其中,k,t,s∈R. ,求函数关系式s=f(t);
,求函数关系式s=f(t); .
.![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() ,求函数关系式
,求函数关系式![]() ;
;![]() ,求s的最大值;
,求s的最大值;![]()