
【题目】已知函数f(x)=(x2-ax+a)e-x,a∈R
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(x)=f’(x),其中f’(x)为函数f(x)的导函数.判断g(x)在定义域内是否为单调函数,并说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)函数求导得f’(x)=-(x-2)(x-a)e-x,讨论a和2的大小,结合导数的正负讨论单调性即可;
(Ⅱ)g’(x)=f"(x)=[x2-(a+4)x+3a+2]×e-x,记h(x)=x2-(a+4)x+3a+2,通过二次函数的性质知函数有正有负,从而得g(x)在定义域内不为单调函数.
试题解析:
(Ⅰ)函数f(x)的定义域为{x|x∈R}. ![]() .
.
①当a<2时,令f’(x)<0,解得:x<a或x>2,f(x)为减函数;
令f’(x)>0,解得:a<x<2,f(x)为增函数.
②当a=2时,f’(x)=-(x-2)2e-x≤0恒成立,函数f(x)为减函数;
③当a>2时,令f’(x)<0,解得:x<2或x>a,函数f(x)为减函数;
令f’(x)>0,解得:2<x<a,函数f(x)为增函数.
综上,
当a<2时,f(x)的单调递减区间为(-∞,a),(2,+∞);单调递增区间为(a,2);
当a=2时,f(x)的单调递减区间为(-∞,+∞);
当a>2时,f(x)的单调递减区间为(-∞,2),(a,+∞);单调递增区间为(2,a).
(Ⅱ)g(x)在定义域内不为单调函数,以下说明:
g’(x)=f"(x)=[x2-(a+4)x+3a+2]×e-x.
记h(x)=x2-(a+4)x+3a+2,则函数h(x)为开口向上的二次函数.
方程h(x)=0的判别式△=a2-4a+8=(a-2)2+4>0恒成立.
所以,h(x)有正有负,从而g’(x)有正有负
故g(x)在定义域内不为单调函数.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的2倍,且过点
的长轴长是短轴长的2倍,且过点![]() .
.
⑴求椭圆![]() 的方程;
的方程;
⑵若在椭圆上有相异的两点![]() (
(![]() 三点不共线),
三点不共线),![]() 为坐标原点,且直线
为坐标原点,且直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率满足
的斜率满足![]() .
.
(ⅰ)求证: ![]() 是定值;
是定值;
(ⅱ)设![]() 的面积为
的面积为![]() ,当
,当![]() 取得最大值时,求直线
取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
科目:高中数学 来源: 题型:
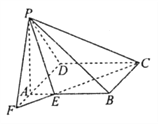
【题目】在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形, ![]() 平面
平面![]() ,
, ![]() 是等腰三角形,
是等腰三角形, ![]() ,
, ![]() 是
是![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ),
),![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正切值
的正切值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,设动点
,设动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() 的重心恰好在圆
的重心恰好在圆![]() 上,求
上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义为R的偶函数,且
是定义为R的偶函数,且![]() 对任意的
对任意的![]() ,都有
,都有![]() 且当
且当![]() 时,
时, ![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰好有3个不同的实数根,则
恰好有3个不同的实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
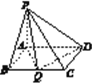
【题目】在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=![]() BC(a>0).
BC(a>0).
(1)当a=1时,求证:BD⊥PC;
(2)若BC边上有且只有一个点Q,使得PQ⊥QD,求此时二面角A-PD-Q的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com