
【题目】已知椭圆C的中心在原点,焦点在x轴上,左、右焦点分别为F1、F2,且|F1F2|=2,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A、B两点,且△AF2B的面积为![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() ;(2)y=±(x+1).
;(2)y=±(x+1).
【解析】试题分析:(1)根据椭圆定义求得2a,再根据焦距得c,解得b(2)先设直线方程,根据点到直线距离得高,联立直线方程与椭圆方程,利用韦达定理与弦长公式得底,最后代入三角形面积公式得k
试题解析:(1)设椭圆的方程为![]() (a>b>0),由题意可得椭圆C两焦点坐标分别为F1(-1,0),F2(1,0).
(a>b>0),由题意可得椭圆C两焦点坐标分别为F1(-1,0),F2(1,0).
∴2a=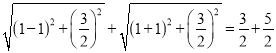
=4.∴a=2,又c=1,∴b2=4-1=3,
故椭圆C的方程为![]()
(2)当直线l⊥x轴时,计算得到:A![]() ,B
,B![]() ,S△AF2B=
,S△AF2B=![]() ·|AB|·|F1F2|=
·|AB|·|F1F2|=![]() ×3×2=3,不符合题意.
×3×2=3,不符合题意.
当直线l与x轴不垂直时,设直线l的方程为:y=k(x+1),代入![]()
消去y得(3+4k2)x2+8k2x+4k2-12=0.
显然Δ>0成立,设A(x1,y1),B(x2,y2),
则x1+x2=-![]() ,x1·x2=
,x1·x2=![]() .
.
又|AB|·![]()
=![]() ·
·![]() =
=![]() ,
,
点F2到AB的距离d=![]() =
=![]() ,
,
所以S△AF2B=![]() |AB|·d=
|AB|·d=![]() ·
·![]() ·
·![]() =
=![]() =
=![]() ,
,
化简,得17k4+k2-18=0,即(k2-1)(17k2+18)=0,解得k=±1.
所以y=±(x+1).


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
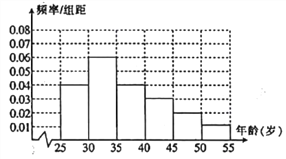
【题目】某高校进行社会实践,对![]() 岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在
岁的人群随机抽取 1000 人进行了一次是否开通“微博”的调查,开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到到各年龄段人数的频率分布直方图如图所示,其中在![]() 岁,
岁, ![]() 岁年龄段人数中,“时尚族”人数分别占本组人数的
岁年龄段人数中,“时尚族”人数分别占本组人数的![]() 、
、![]() .
.
(1)求![]() 岁与
岁与![]() 岁年龄段“时尚族”的人数;
岁年龄段“时尚族”的人数;
(2)从![]() 岁和
岁和![]() 岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在
岁年龄段的“时尚族”中,采用分层抽样法抽取6人参加网络时尚达人大赛,其中两人作为领队.求领队的两人年龄都在![]() 岁内的概率。
岁内的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E. 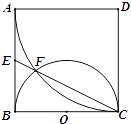
(1)求证:AE=EB;
(2)求EFFC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
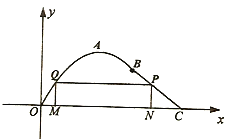
【题目】如图在长为10千米的河流![]() 的一侧有一条观光带,观光带的前一部分为曲线段
的一侧有一条观光带,观光带的前一部分为曲线段![]() ,设曲线段
,设曲线段![]() 为函数
为函数![]() (单位:千米)的图象,且图象的最高点为
(单位:千米)的图象,且图象的最高点为![]() ;观光带的后一部分为线段
;观光带的后一部分为线段![]() .
.
(1)求函数为曲线段![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)若计划在河流![]() 和观光带
和观光带![]() 之间新建一个如图所示的矩形绿化带
之间新建一个如图所示的矩形绿化带![]() ,绿化带仅由线段
,绿化带仅由线段![]() 构成,其中点
构成,其中点![]() 在线段
在线段![]() 上.当
上.当![]() 长为多少时,绿化带的总长度最长?
长为多少时,绿化带的总长度最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BD是等腰直角三角形△ABC腰AC上的中线,AM⊥BD于点M,延长AM交BC于点N,AF⊥BC于点F,AF与BD交于点E.
(1)求证;△ABE≌△ACN;
(2)求证:∠ADB=∠CDN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com