
【题目】已知函数f(x)=x﹣alnx+b,a,b为实数.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+3,求a,b的值;
(Ⅱ)若|f′(x)|< ![]() 对x∈[2,3]恒成立,求a的取值范围.
对x∈[2,3]恒成立,求a的取值范围.
【答案】解:(I)f′(x)=1﹣ ![]() , ∵曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+3,
, ∵曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+3,
∴f′(1)=2,f(1)=5,
∴ ![]() ,解得a=﹣1,b=4.
,解得a=﹣1,b=4.
(II)∵|f′(x)|< ![]() 对x∈[2,3]恒成立,即|1﹣
对x∈[2,3]恒成立,即|1﹣ ![]() |<
|< ![]() 对x∈[2,3]恒成立,
对x∈[2,3]恒成立,
∴|x﹣a|< ![]() 对x∈[2,3]恒成立,
对x∈[2,3]恒成立,
∴x﹣ ![]() <a<x+
<a<x+ ![]() 对x∈[2,3]恒成立,
对x∈[2,3]恒成立,
设g(x)=x﹣ ![]() ,h(x)=x+
,h(x)=x+ ![]() ,x∈[2,3],
,x∈[2,3],
则g′(x)=1+ ![]() >0,h′(x)=1﹣
>0,h′(x)=1﹣ ![]() >0,
>0,
∴g(x)在[2,3]上是增函数,h(x)在[2,3]上是增函数,
∴gmax(x)=g(3)=2,hmin(x)=h(2)= ![]() 三.
三.
∴a的取值范围是[2, ![]() ].
].
【解析】(I)根据导数的几何意义可得f′(1)=2,f(1)=5,列方程组解出a,b即可;(II)分离参数得出x﹣ ![]() <a<x+
<a<x+ ![]() ,分别求出左侧函数的最大值和右侧函数的最小值即可得出a的范围.
,分别求出左侧函数的最大值和右侧函数的最小值即可得出a的范围.


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() ,一等轴双曲线的顶点是该椭圆的焦点,设
,一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() .
.

(1)求椭圆和双曲线的标准方程;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() 为定值;
为定值;
(3)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x)为减函数,且函数y=f(x﹣1)的图象关于点(1,0)对称,若f(x2﹣2x)+f(2b﹣b2)≤0,且0≤x≤2,则x﹣b的取值范围是( )
A.[﹣2,0]
B.[﹣2,2]
C.[0,2]
D.[0,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
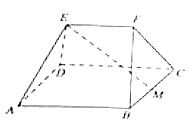
【题目】如图,在多面体ABCDEF中,四边形ABCD为边长为4的正方形,M是BC的中点,EF∥平面ABCD,且EF=2,AE=DE=BF=CF= ![]() .
. 
(1)求证:ME⊥平面ADE;
(2)求二面角B﹣AE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工艺厂有铜丝5万米,铁丝9万米,准备用这两种材料编制成花篮和花盆出售,已知一只花篮需要用铜丝200米,铁丝300米;编制一只花盆需要100米,铁丝300米,设该厂用所有原来编制个花篮![]() ,
, ![]() 个花盆.
个花盆.
(Ⅰ)列出![]() 满足的关系式,并画出相应的平面区域;
满足的关系式,并画出相应的平面区域;
(Ⅱ)若出售一个花篮可获利300元,出售一个花盘可获利200元,那么怎样安排花篮与花盆的编制个数,可使得所得利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第三章“衰分”介绍比例分配问题:“衰分”是按比例递减分配的意思,通常称递减的比例(百分比)为“衰分比”.如:甲、乙、丙、丁衰分得100,60,36,21.6个单位,递减的比例为40%,今共有粮m(m>0)石,按甲、乙、丙、丁的顺序进行“衰分”,已知丙衰分得80石,乙、丁衰分所得的和为164石,则“衰分比”与m的值分别为( )
A.20% 369
B.80% 369
C.40% 360
D.60% 365
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com