Question

【题目】为比较甲、乙两地某月14时的气温状况，随机选取该月中的5天，将这5天中14时的气温数据（单位：℃）制成如图所示的茎叶图.考虑以下结论：

①甲地该月14时的平均气温低于乙地该月14时的平均气温；

②甲地该月14时的平均气温高于乙地该月14时的平均气温；

③甲地该月14时的平均气温的标准差小于乙地该月14时的气温的标准差；

④甲地该月14时的平均气温的标准差大于乙地该月14时的气温的标准差.

其中根据茎叶图能得到的统计结论的标号为（ ）

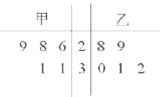
A.①③B.①④C.②③D.②④

Answer 1

【答案】B

【解析】

根据茎叶图中数据，结合平均数与方差的计算公式即可求出结果，属于常考题型.

由茎叶图中的数据，我们可得甲、乙两地某月14时的气温抽取的样本温度分别为：

甲：26，28，29，31，31；乙：28，29，30，31，32；

所以，甲地该月14时的平均气温为：；

乙地该月14时的平均气温为：；故；即①正确；

又甲地该月14时温度的方差为：

乙地该月14时温度的方差为：

；

故；即④正确.

故选：B