练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是（ ）

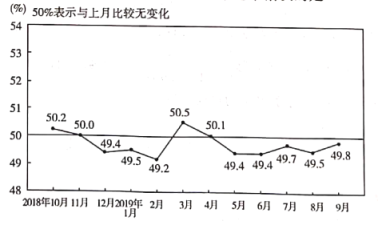
    A.12个月的PMI值不低于50%的频率为

    B.12个月的PMI值的平均值低于50%

    C.12个月的PMI值的众数为49.4%

    D.12个月的PMI值的中位数为50.3%

    【答案】D

    【解析】

    根据图形中的信息，可得频率、平均值的估计、众数、中位数，从而得到答案.

    对A，从图中数据变化看，PMI值不低于50%的月份有4个，所以12个月的PMI值不低于50%的频率为，故A正确；

    对B，由图可以看出，PMI值的平均值低于50%，故B正确；

    对C，12个月的PMI值的众数为49.4%，故C正确，；

    对D，12个月的PMI值的中位数为49.6%，故D错误

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列结论：在回归分析中

    （1）可用相关指数的值判断模型的拟合效果，越大，模型的拟合效果越好；

    （2）可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；

    （3）可用相关系数的值判断模型的拟合效果，越大，模型的拟合效果越好；

    （4）可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比较合适．带状区域的宽度越窄，说明模型的拟合精度越高.

    以上结论中，不正确的是（ ）

    A.（1）（3）B.（2）（3）C.（1）（4）D.（3）（4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】出版商为了解某科普书一个季度的销售量（单位：千本）和利润（单位：元/本）之间的关系，对近年来几次调价之后的季销售量进行统计分析，得到如下的10组数据.

    序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    2.4

    3.1

    4.6

    5.3

    6.4

    7.1

    7.8

    8.8

    9.5

    10

    18.1

    14.1

    9.1

    7.1

    4.8

    3.8

    3.2

    2.3

    2.1

    1.4

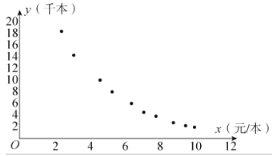
    根据上述数据画出如图所示的散点图：

    （1）根据图中所示的散点图判断和哪个更适宜作为销售量关于利润的回归方程类型？（给出判断即可，不需要说明理由）

    （2）根据（1）中的判断结果及参考数据，求出关于的回归方程；

    （3）根据回归方程预测当每本书的利润为10.5元时的季销售量.

    参考公式及参考数据：

    ①对于一组数据，其回归直线的斜率和截距的公式分别为.

    ②参考数据：

    6.50

    6.60

    1.75

    82.50

    2.70

    表中.另：.计算时，所有的小数都精确到0.01.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】月份的二中迎来了国内外的众多宾客，其中很多人喜欢询问团队模式，为了了解“询问团队模式”是否与性别有关，在月期间，随机抽取了人，得到如下所示的列联表：

    关心“团队”

    不关心“团队”

    合计

    男性

    12

    女性

    36

    合计

    80

    （1）若在这人中，按性别分层抽取一个容量为的样本，男性应抽人，请将上面的列联表补充完整，并据此资料能否在犯错误的概率不超过前提下，认为关心“团队”与性别有关系？

    （2）若以抽取样本的频率为概率，从月来宾中随机抽取人赠送精美纪念品，记这人中关心“团队”人数为，求的分布列和数学期望.

    附：

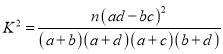
    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】凤鸣山中学的高中女生体重 (单位：kg)与身高(单位：cm)具有线性相关关系，根据一组样本数据（），用最小二乘法近似得到回归直线方程为，则下列结论中不正确的是（ ）

    A.与具有正线性相关关系

    B.回归直线过样本的中心点

    C.若该中学某高中女生身高增加1cm，则其体重约增加0.85kg

    D.若该中学某高中女生身高为160cm，则可断定其体重必为50.29kg.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近几年一种新奇水果深受广大消费者的喜爱，一位农户发挥聪明才智，把这种露天种植的新奇水果搬到了大棚里，收到了很好的经济效益．根据资料显示，产出的新奇水果的箱数x（单位：十箱）与成本y（单位：千元）的关系如下：

    x

    1

    3

    4

    6

    7

    y

    5

    6．5

    7

    7．5

    8

    y与x可用回归方程 （ 其中，为常数）进行模拟．

    （Ⅰ）若该农户产出的该新奇水果的价格为150元/箱，试预测该新奇水果100箱的利润是多少元．|．

    （Ⅱ）据统计，10月份的连续16天中该农户每天为甲地配送的该新奇水果的箱数的频率分布直方图如图所示．

    （i）若从箱数在内的天数中随机抽取2天，估计恰有1天的水果箱数在内的概率；

    （ⅱ）求这16天该农户每天为甲地配送的该新奇水果的箱数的平均值．（每组用该组区间的中点值作代表）

    参考数据与公式：设，则

    0.54

    6.8

    1.53

    0.45

    线性回归直线中，，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以直角坐标系的原点为极坐标系的极点，轴的正半轴为极轴．已知曲线的极坐标方程为，是上一动点，，点的轨迹为．

    （1）求曲线的极坐标方程，并化为直角坐标方程；

    （2）若点，直线的参数方程（为参数），直线与曲线的交点为，当取最小值时，求直线的普通方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

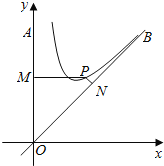
    【题目】如图，是南北方向的一条公路，是北偏东方向的一条公路，某风景区的一段边界为曲线．为方便游客光，拟过曲线上的某点分别修建与公路，垂直的两条道路，，且，的造价分别为5万元百米，40万元百米，建立如图所示的直角坐标系，则曲线符合函数模型，设，修建两条道路，的总造价为万元，题中所涉及的长度单位均为百米．

    （1）求解析式；

    （2）当为多少时，总造价最低？并求出最低造价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(0，－2)，椭圆E： (a>b>0)的离心率为，F是椭圆E的右焦点，直线AF的斜率为，O为坐标原点.

    (1)求E的方程；

    (2)设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

    查看答案和解析>>

    同步练习册答案