
 .
.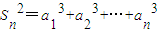 (n∈N*).从而
(n∈N*).从而 ,两式相减,得
,两式相减,得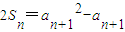 ,再写一式,两式相减,可得数列{an}的任一项an与它的前一项an-1间的递推关系;利用a1=1,a2013=-2012,所以无穷数列{an}的前2012项组成首项和公差均为1的等差数列,从第2013项开始组成首项为-2012,公比为-1的等比数列,从而可得数列的通项.
,再写一式,两式相减,可得数列{an}的任一项an与它的前一项an-1间的递推关系;利用a1=1,a2013=-2012,所以无穷数列{an}的前2012项组成首项和公差均为1的等差数列,从第2013项开始组成首项为-2012,公比为-1的等比数列,从而可得数列的通项.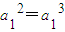 ,由a1≠0得a1=1.(1分)
,由a1≠0得a1=1.(1分)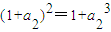 ,由a2≠0得a2=2或a2=-1.
,由a2≠0得a2=2或a2=-1.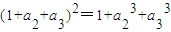 ,若a2=2得a3=3或a3=-2;若a2=-1得a3=1;(5分)
,若a2=2得a3=3或a3=-2;若a2=-1得a3=1;(5分)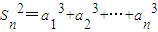 (n∈N*).
(n∈N*).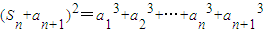 .(7分)
.(7分)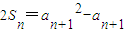 .(8分)
.(8分)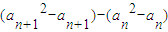 ,即(an+1+an)(an+1-an-1)=0,
,即(an+1+an)(an+1-an-1)=0,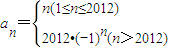 .(14分)
.(14分)

科目:高中数学 来源: 题型:
| 2n |
| 3n+1 |
| 3 |
| 5 |
| 11 |
| 17 |
查看答案和解析>>
科目:高中数学 来源:江西省赣县中学2011届高三适应性考试数学理科试题 题型:013
已知数列{an}的通项为an=3n+8,下列各选项中的数为数列{an}中的项的是
8
16
32
36
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第6章 数列):6.1 数列定义与通项(解析版) 题型:解答题
 ,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1)
,则下列各数是否为数列中的项?如果是,是第几项?如果不是,为什么?(1) (2)
(2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com