
【题目】已知椭圆 ![]() =1的一个焦点为F(2,0),且离心率为
=1的一个焦点为F(2,0),且离心率为 ![]()
(1)求椭圆方程;
(2)过点M(3,0)作直线与椭圆交于A,B两点,求△OAB面积的最大值.
【答案】
(1)解:依题意有c=2, ![]() =
= ![]() ,又a2=b2+c2,
,又a2=b2+c2,
可得a2=6,b2=2.
故椭圆方程为 ![]() =1.
=1.
(2)解:由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x﹣3).
联立方程组 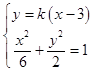 ,消去x得(1+3k2)y2+6ky+3k2=0,
,消去x得(1+3k2)y2+6ky+3k2=0,
∴y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,
,
∴S△OAB= ![]() |OM||y1﹣y2|=
|OM||y1﹣y2|= ![]() ×3×
×3× ![]()
= ![]() 3
3 ![]() =3
=3 ![]() =3
=3 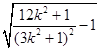 ,
,
令3k2+1=t≥1,则S△OAB=3 ![]() =3
=3 ![]() ≤
≤ ![]() ,当且仅当t=
,当且仅当t= ![]() ,即k2=
,即k2= ![]() ,k=
,k= ![]() 时取等号.
时取等号.
∴△OAB面积的最大值为 ![]() .
.
【解析】(1)依题意有c=2, ![]() =
= ![]() ,又a2=b2+c2,联立解出即可得出.(2)由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x﹣3).与椭圆方程联立可得(1+3k2)y2+6ky+3k2=0,利用根与系数的关系可得:S△OAB=
,又a2=b2+c2,联立解出即可得出.(2)由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x﹣3).与椭圆方程联立可得(1+3k2)y2+6ky+3k2=0,利用根与系数的关系可得:S△OAB= ![]() |OM||y1﹣2|=3
|OM||y1﹣2|=3 ![]() =3
=3 ![]() ,令3k2+1=t≥1,可得S△OAB=3
,令3k2+1=t≥1,可得S△OAB=3 ![]() =3
=3 ![]() ,利用二次函数的单调性即可得出.
,利用二次函数的单调性即可得出.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】下面是关于公差d>0的等差数列{an}的四个命题:p1:数列{an}是递增数列;p2:数列{an}的前n项和Sn是递增数列;p3:数列{ ![]() }是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为( )
}是递增数列;p4:数列{an+nd}是递增数列.其中的真命题为( )
A.p1 , p2
B.p3 , p4
C.p2 , p3
D.p1 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣5|﹣|x﹣2|.
(1)若x∈R,使得f(x)≤m成立,求m的范围;
(2)求不等式x2﹣8x+15+f(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记X表示两人中进入决赛的人数,求X的分布列及数学期望;
(Ⅲ)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.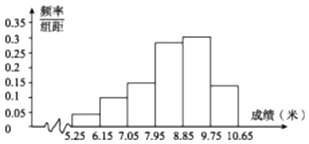
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y= ![]() sin(2x﹣
sin(2x﹣ ![]() )的图象,只需将函数y=sinxcosx的图象( )
)的图象,只需将函数y=sinxcosx的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种, 方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(Ⅰ)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=8x的焦点为F,准线l与x轴的交点为M,过点M的直线l′与抛物线C的交点为P,Q,延长PF交抛物线C于点A,延长QF交抛物线C于点B,若 ![]() +
+ ![]() =22,则直线l′的方程为 .
=22,则直线l′的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axln(x+1)+x+1(x>﹣1,a∈R).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)当x≥0时,不等式f(x)≤ex恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an=3an﹣1+3n﹣1(n∈N* , n≥2), 已知a3=95.
(1)求a1 , a2;
(2)是否存在一个实数t,使得 ![]() ,且{bn}为等差数列?若存在,则求出t的值;若不存在,请说明理由.
,且{bn}为等差数列?若存在,则求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com