
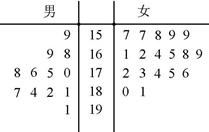
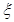 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出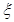 的分布列,并求
的分布列,并求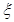 的数学期望.
的数学期望.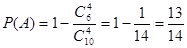 ;(2)分布列为:
;(2)分布列为: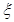 | 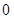 | 1 | 2 | 3 |
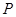 | 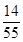 | 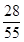 | 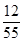 | 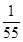 |
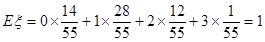
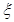 的取值为
的取值为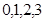 ,那么结合随机变量的概率公式,得到分布列。
,那么结合随机变量的概率公式,得到分布列。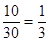 ,所以选中的运动健将有
,所以选中的运动健将有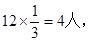
 -----------------3分
-----------------3分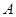 :至少有1名‘运动健将’被选中,则
:至少有1名‘运动健将’被选中,则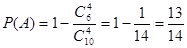
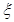 的取值为
的取值为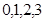
 ----------9分
----------9分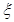 的分布列为:
的分布列为: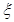 | 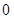 | 1 | 2 | 3 |
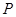 | 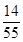 | 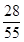 | 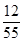 | 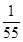 |
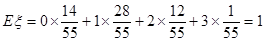 -------------- 12分
-------------- 12分

科目:高中数学 来源:不详 题型:填空题
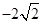 、
、 、
、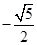 、0、
、0、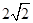 、
、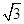 、
、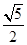 ,用ξ表示坐标原点到直线l的距离,则随机变量ξ的数学期望Eξ=_________.
,用ξ表示坐标原点到直线l的距离,则随机变量ξ的数学期望Eξ=_________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
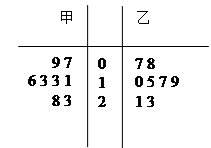
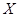 的分布列和均值.(8分)
的分布列和均值.(8分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

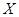 表示至第2分钟末已办理完业务的顾客人数,求
表示至第2分钟末已办理完业务的顾客人数,求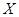 的分布列及数学期望
的分布列及数学期望查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
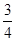 ,命中得
,命中得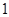 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为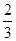 ,每命中一次得
,每命中一次得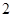 分,没有命中得
分,没有命中得 分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.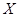 的分布列及数学期望
的分布列及数学期望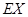 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com