
【题目】政府为了对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如图列联表,已知样本中城市人数与农村人数之比是![]() ;
;
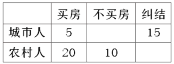
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
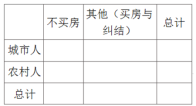
(Ⅱ)请完成列联表,并用独立性检验的思想方法说明有多少的把握认为不买房心理预期与城乡有关?
参考公式: ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(Ⅰ)城市人中的不买房人数和农村人中的纠结人数分别是![]() ,
,![]() 人;(Ⅱ)列联表详见解析,有
人;(Ⅱ)列联表详见解析,有![]() 的把握认为不买房与城乡有关.
的把握认为不买房与城乡有关.
【解析】
(Ⅰ)通过样本中城市人数与农村人数之比是![]() 与表格中的数据列出等式组,可得解;
与表格中的数据列出等式组,可得解;
(Ⅱ)由(Ⅰ)中数据得到列联表,根据![]() 的计算公式,及表格中的临界值判定,即得解.
的计算公式,及表格中的临界值判定,即得解.
解:(Ⅰ)设城市人中的不买房人数和农村人中的纠结人数分别是![]() ,
,![]() 人,
人,
则 解得
解得![]()
即城市人中的不买房人数和农村人中的纠结人数分别是![]() ,
,![]() 人
人
(Ⅱ)设不买房心理预期与城乡无关,由(Ⅰ)得到如下的列联表:
不买房 | 其他(买房与纠结) | 总计 | |
城市人 | 10 | 20 | 30 |
农村人 | 10 | 70 | 80 |
总计 | 20 | 90 | 110 |
对于上述不买房心理预期构造一个随机变量![]() .由表中数据可得,
.由表中数据可得,
![]() .
.
所以有![]() 的把握认为不买房与城乡有关.
的把握认为不买房与城乡有关.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
B.函数![]() 在区间
在区间![]() 上单调递减
上单调递减
C.函数![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]()
D.存在某一个实数![]() 的值,使得函数
的值,使得函数![]() 是偶函数
是偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知王明比较喜爱打篮球,近来,他为了提高自己的投篮水平,制定了一个夏季训练计划.班主任为了了解其训练效果,开始训练前,统计了王明![]() 场比赛的得分,计算出得分数据的中位数为
场比赛的得分,计算出得分数据的中位数为![]() 分,平均得分为
分,平均得分为![]() 分,得分数据的方差为
分,得分数据的方差为![]() ,训练结束后统计了
,训练结束后统计了![]() 场比赛得分成绩茎叶图如下图:
场比赛得分成绩茎叶图如下图:
![]()
(1)求王明训练结束后统计的![]() 场比赛得分的中位数,平均得分以及方差;
场比赛得分的中位数,平均得分以及方差;
(2)若只从训练前后统计的各![]() 场比赛得分数据分析,训练计划对王明投篮水平的提高是否有帮助?
场比赛得分数据分析,训练计划对王明投篮水平的提高是否有帮助?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com