
分析 (1)依题意|OA|=4sinφ,$|{OB}|=4sin({φ+\frac{π}{4}}),|{OC}|=4sin({φ-\frac{π}{4}})$,利用三角恒等变换化简|OB|+|OC|为$4\sqrt{2}sinφ=\sqrt{2}|{OA}|$,命题得证.
(2)当$φ=\frac{5π}{12}$时,B,C两点的极坐标分别为$({2\sqrt{3},\frac{2π}{3}}),({2,\frac{π}{6}})$,再把它们化为直角坐标,根据C2是经过点(m,0),倾斜角为α的直线,又经过点B,C的直线方程为$y=-\frac{{\sqrt{3}}}{3}x+2$,由此可得m及直线的斜率,从而求得α的值.
解答 (1)证明:依题意|OA|=4sinφ,$|{OB}|=4sin({φ+\frac{π}{4}}),|{OC}|=4sin({φ-\frac{π}{4}})$,
则$|{OB}|+|{OC}|=4sin({φ+\frac{π}{4}})+4sin({φ-\frac{π}{4}})=2\sqrt{2}({sinφ+cosφ})+2\sqrt{2}({sinφ-cosφ})$=$4\sqrt{2}sinφ=\sqrt{2}|{OA}|$;
(2)解:当$φ=\frac{5π}{12}$时,B,C两点的极坐标分别为$({2\sqrt{3},\frac{2π}{3}}),({2,\frac{π}{6}})$,
化为直角坐标为$B({-\sqrt{3},3}),C({\sqrt{3},1})$,
曲线C2是经过点(m,0),且倾斜角为α的直线,又因为经过点B,C的直线方程为$y=-\frac{{\sqrt{3}}}{3}x+2$,
所以$m=2\sqrt{3},α=\frac{5π}{6}$.
点评 本题主要考查把参数方程化为直角坐标方程,把点的极坐标化为直角坐标,直线的倾斜角和斜率,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
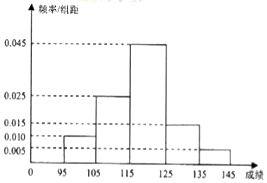 高二数学ICTS竞赛初赛考试后,某校对95分以上的成绩进行统计,其频率分布直方图如图所示,其中[135,145]分数段的人数为2人.
高二数学ICTS竞赛初赛考试后,某校对95分以上的成绩进行统计,其频率分布直方图如图所示,其中[135,145]分数段的人数为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
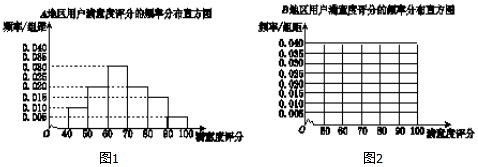
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 8 | 14 | 10 | 6 |
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com