练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．过点P（3，1）向圆（x-1）2+y2=1作两条切线PA，PB，切点分别为A，B，则弦AB所在直线的方程为2x+y-3=0．

    分析 求出以（3，1）、C（1，0）为直径的圆的方程，将两圆的方程相减可得公共弦AB的方程．

    解答 解：圆（x-1）2+y2=1的圆心为C（1，0），半径为1，
    以（3，1）、C（1，0）为直径的圆的方程为（x-2）2+（y-$\frac{1}{2}$）2=$\frac{5}{4}$，
    将两圆的方程相减可得公共弦AB的方程2x+y-3=0，
    故答案为：2x+y-3=0．

    点评 本题考查直线和圆的位置关系以及圆和圆的位置关系、圆的切线性质，体现了数形结合的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

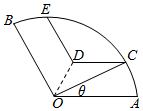    8．如图，扇形AOB是一个植物园的平面示意图，其中∠AOB=$\frac{2π}{3}$，半径OA=OB=1km，为了便于游客观赏，拟在圆内铺设一条从入口A到出口B的观赏道路，道路由弧$\widehat{AC}$，线段CD，线段DE和弧$\widehat{EB}$组成，且满足：$\widehat{AC}$=$\widehat{EB}$，CD∥AO．DE∥OB，OD∈[$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{6}}{3}$]（单位：km），设∠AOC=θ．
    （1）用θ表示CD的长度，并求出θ的取值范围；
    （2）当θ为何值时，观赏道路最长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知集合M和N间的关系为M∩N=M，那么下列必定成立的是（　　）
    A．∁UN∩M=∅B．∁UM∩N=∅C．∁UM∩∁UN=∅D．∁UM∪∁UN=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

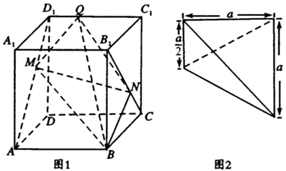
    6．如图1，已知正方体ABCD-A1B1C1D1的棱长为a，M，N，Q分别是线段AD1，B1C，C1D1上的动点，当三棱锥Q-BMN的俯视图如图2所示时，三棱锥Q-BMN的体积为（　　）
    A．$\frac{1}{2}{a^3}$B．$\frac{1}{4}{a^3}$C．$\frac{{\sqrt{2}}}{4}{a^3}$D．$\frac{1}{12}{a^3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=b•ax（a＞0，a≠1，b∈R）的图象经过点A（1，$\frac{1}{2}$），B（3，2）
    （1）试确定f（x）的解析式；
    （2）记集合E={y|y=bx-（$\frac{1}{a}$）x+1，x∈[-3，2]}，λ=（$\frac{1}{10}$）0+${8^{-\frac{2}{3}}}$+$\root{3}{{{{（-\frac{3}{4}）}^3}}}$，判断λ与E的关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知等差数列{an}的前n项和为Sn，且S3=6，S5=15．
    （1）求数列{an}的通项公式；
    （2）令bn=2an，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知全集U={1，2，3，4}，集合A={2，3}，B={3，4}，则（∁UA）∩（∁UB）={1}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某班50位学生期中考试数学成绩的频率直方分布图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
    （1）求图中x的值；
    （2）根据频率直方分布图计算该班50位学生期中考试数学成绩的平均数与中位数（精确到个位）；
    （3）从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为X，求P（X=1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知a，b，c为正实数，给出以下结论：
    ①若a-2b+3c=0，则$\frac{{b}^{2}}{ac}$的最小值是3；
    ②若a+2b+2ab=8，则a+2b的最小值是4；
    ③若a（a+b+c）+bc=4，则2a+b+c的最小是2$\sqrt{3}$；
    ④若a2+b2+c2=4，则ab+bc的最大值是2$\sqrt{2}$．
    其中正确结论的序号是①②④．

    查看答案和解析>>

    同步练习册答案