练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数F（x）=|lgx|，若0＜a＜b，且f（a）=f（b），则a+2b的取值范围是（ ）
    A.
    B.
    C.（3，+∞）
    D.[3，+∞）

    【答案】C
    【解析】解答：因为f（a）=f（b），所以|lga|=|lgb|，所以a=b（舍去），或 ，所以a+2b= 又0＜a＜b，所以0＜a＜1＜b，令 ，由“对勾”函数的性质知函数f（a）在a∈（0，1）上为减函数，所以f（a）＞f（1）=1+ =3，即a+2b的取值范围是（3，+∞）．
    故选C．
    分析：由题意f（a）=f（b），求出ab的关系，然后利用“对勾”函数的性质知函数f（a）在a∈（0，1）上为减函数，确定a+2b的取值范围．
    【考点精析】本题主要考查了基本不等式的相关知识点，需要掌握基本不等式：,（当且仅当时取到等号）；变形公式：才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若定义在R上的函数 满足 ，其导函数 满足 ，则下列结论中一定错误的是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在圆上任取一点，过点向轴作垂线段，垂足为，当点在圆上运动时，线段的中点的轨迹为.

    (1)求曲线的方程；

    (2)过点(0，－2)作直线与交于两点，(O为原点)，求三角形面积的最大值，并求此时的直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 为等差数列，公差 （ ），且（ ）
    （1）求证：当 取不同自然数时，此方程有公共根；
    （2）若方程不同的根依次为 ， ， ， …， ， …，求证：数列 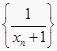为等差数列。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一列火车从重庆驶往北京，沿途有n个车站（包括起点站重庆和终点站北京）．车上有一邮政车厢，每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个，同时又要装上该站发往以后各站的邮袋各1个，设从第k站出发时，邮政车厢内共有邮袋ak个（k=1，2，…，n）．
    （1）求数列{ak}的通项公式；
    （2）当k为何值时，ak的值最大，求出ak的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，最小值为4的有多少个？（ ） ① ② （0＜x＜π） ③y=ex+4e﹣x④y=log3x+4logx3．
    A.4
    B.3
    C.2
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若直线ax﹣by+2=0（a＞0，b＞0）和函数f（x）=ax+1+1（a＞0且a≠1）的图象恒过同一个定点，则当 + 取最小值时，函数f（x）的解析式是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在下列命题中，下列选项正确的是（ ）

    A. 在回归直线中，变量时，变量的值一定是15.

    B. 两个变量相关性越强，则相关系数就越接近于1.

    C. 在残差图中，残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适，与带状区域的宽度无关.

    D. 若是两个相等的非零实数，则是纯虚数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=x2﹣bx+alnx．
    （1）若b=2，函数f（x）有两个极值点x1 ， x2 ， 且x1＜x2 ， 求实数a的取值范围；
    （2）在（1）的条件下，证明：f（x2）＞﹣ ；
    （3）若对任意b∈[1，2]，都存在x∈（1，e）（e为自然对数的底数），使得f（x）＜0成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案