练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知四边形为等腰梯形，∥，沿对角线将旋转，使得点至点的位置，此时满足.

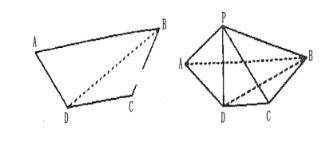
    （1）证明；

    （2）求二面角平面角的正弦值.

    【答案】（1）详见解析；（2）.

    【解析】

    (1）先由余弦定理的计算得到 ,

    折叠后，又，故面，根据折叠后不变的一些垂直关系证得面，进而得到结论.

    （2）建立空间直角坐标系，用坐标表示向量，求得平面的法向量与平面的法向量，计算再求得正弦即可.

    解：（1） 证明：在等腰梯形中，由平面几何知识易得，又，由余弦定理可得，则，故,

    折叠后，又，故面，

    而面，故.

    （2）由（1）知面，，以点为坐标原点，以所在的直线分别为轴建立如图所示的空间直角坐标系，

    则

    则，

    设平面的法向量为，则即.

    取则故

    同理可求得平面的法向量

    设二面角的平面角为，则，

    结合图形可知.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，求证：

    （1）在区间存在唯一极大值点；

    （2）在上有且仅有2个零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的极值；

    （2）设函数，若存在，使，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数y＝f（x）与函数y＝g（x）的图象如图所示，则函数y＝f（x）g（x）的图象可能是下面的（　　）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2－mlnx，h(x)＝x2－x＋a.

    (1)当a＝0时，f(x)≥h(x)在(1，＋∞)上恒成立，求实数m的取值范围；

    (2)当m＝2时，若函数k(x)＝f(x)－h(x)在区间(1,3)上恰有两个不同零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合，，映射,使得，已知，.则x,y,u的值分别是____.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在件产品中，有件正品，件次品，从这件产品中任意抽取件.

    （1）共有多少种不同的抽法？

    （2）抽出的件中恰有件次品的抽法有多少种？

    （3）抽出的件中至少有件次品的抽法有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果在一条平面曲线上存在四点，使得这四点构成的图形是一个菱形，则称该曲线存在内接菱形．现已知双曲线，双曲线，其中，，．证明：在双曲线与中有且仅有一条存在内接菱形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有四名男生，三名女生排队照相，七个人排成一排，则下列说法正确的有（ ）

    A.如果四名男生必须连排在一起，那么有种不同排法

    B.如果三名女生必须连排在一起，那么有种不同排法

    C.如果女生不能站在两端，那么有种不同排法

    D.如果三个女生中任何两个均不能排在一起，那么有种不同排法

    查看答案和解析>>

    同步练习册答案