
| A. | 15 | B. | 30 | C. | 45 | D. | 75 |
分析 在准备的两个问题中每一个问题被问到的概率相同,第一个问题可能被询问150次,在被询问的150中有75人学号是奇数,比90人多出来的人数就是闯过红灯的人数,按照比例得到结果.
解答 解:要调查300名学生,
在准备的两个问题中每一个问题被问到的概率相同,
∴第一个问题可能被询问150次,
∵在被询问的150人中有75人学号是奇数,而有90人回答了“是”,
∴估计有15个人闯过红灯,即在150人中有15个人闯红灯,
∴根据概率的知识来计算这300人中有过闯过红灯的人数为15×2=30,
故选:B.
点评 本题考查实际推断原理和假设检验,是一个基础题,但是题干比较长,这样给我们读懂题意带来困难,不能弄懂题意是本题的难点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
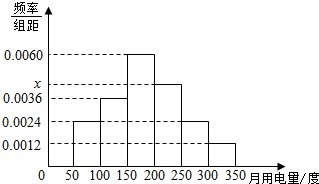 为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.
为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\frac{5}{4}$x | B. | y=$±\frac{4}{5}$x | C. | y=$±\frac{3}{4}$x | D. | y=$±\frac{4}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com