
【题目】某校的1000名高三学生参加四门学科的选拔考试,每门试卷共有10道题,每题10分,规定:每门错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,在录取时,
,在录取时,![]() 记为90分,
记为90分,![]() 记为80分,
记为80分,![]() 记为60分,
记为60分,![]() 记为50分.
记为50分.
根据模拟成绩,每一门都有如下统计表:
答错 题数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 90 | 100 | 150 | 150 | 200 | 100 | 100 | 50 | 49 | 1 |
已知选拔性考试成绩与模拟成绩基本吻合.
(1)设![]() 为高三学生一门学科的得分,求
为高三学生一门学科的得分,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)预测考生4门总分为320概率.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知一个袋子里有形状一样仅颜色不同的6个小球,其中白球2个,黑球4个![]() 现从中随机取球,每次只取一球.
现从中随机取球,每次只取一球.
![]() 若每次取球后都放回袋中,求事件“连续取球四次,至少取得两次白球”的概率;
若每次取球后都放回袋中,求事件“连续取球四次,至少取得两次白球”的概率;
![]() 若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望.
若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且右焦点为
,且右焦点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .若
.若![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)在(2)的条件下,若点![]() 不在椭圆
不在椭圆![]() 的内部,点
的内部,点![]() 是点
是点![]() 关于原点
关于原点![]() 的对称点,试求三角形
的对称点,试求三角形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两班各随机抽取10名同学,下面的茎叶图记录了这20名同学在2018年高考语文作文题目中的成绩(单位:分).已知语文作文题目满分为60分,“分数![]() 分,为及格;分数
分,为及格;分数![]() 分,为高分”,若甲、乙两班的成绩的平均分都是44分,
分,为高分”,若甲、乙两班的成绩的平均分都是44分,
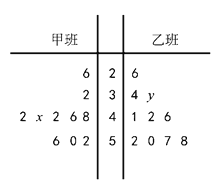
(1)求![]() 的值;
的值;
(2)若分别从甲、乙两班随机各抽取1名成绩为高分的学生,求抽到的学生中,甲班学生成绩高于乙班学生成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人.”其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人.”在该问题中的1864人全部派遣到位需要的天数为( )
A. 9B. 16C. 18D. 20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()

(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲袋中装有3个白球和5个黑球,乙袋中装有4个白球和6个黑球,现从甲袋中随机取出一个球放入乙袋中,充分混合后,再从乙袋中随机取出一个球放回甲袋中,则甲袋中白球没有减少的概率为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com