
【题目】如图,函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0≤φ≤![]() )的部分图象,其图象与y轴交于点(0,
)的部分图象,其图象与y轴交于点(0,![]() )
)
(Ⅰ)求函数的解析式;
(Ⅱ)若![]() , 求
, 求![]() -
-![]() 的值.
的值.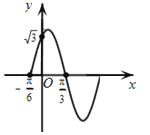
【答案】解:( I)∵0≤φ≤![]() ,
,
∴由五点对应法得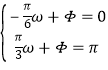 ,解得ω=2,φ=
,解得ω=2,φ=![]() ,
,
则f(x)=Asin(ωx+φ)=Asin(2x+![]() ),
),
∵图象与y轴交于点(0,![]() ),
),
∴f(0)=Asin![]() =
=![]() ,解得A=2,
,解得A=2,
故![]() .
.
( II)∵![]() =1,
=1,
∴得![]() ,
,
则![]()
![]() -=
-=![]() -
-![]() =
=![]() -
-![]() -
-![]() =-8.
=-8.
【解析】(Ⅰ)根据图象确定A,ω 和φ的值即可求函数的解析式;
(Ⅱ)利用三角函数的诱导公式进行化简即可.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,左焦点是
,左焦点是![]() .
.
(1)若左焦点![]() 与椭圆
与椭圆![]() 的短轴的两个端点是正三角形的三个顶点,点
的短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上.求椭圆
上.求椭圆![]() 的方程;
的方程;
(2)过原点且斜率为![]() 的直线
的直线![]() 与(1)中的椭圆
与(1)中的椭圆![]() 交于不同的两点
交于不同的两点![]() ,设
,设![]() ,求四边形
,求四边形![]() 的面积取得最大值时直线
的面积取得最大值时直线![]() 的方程;
的方程;
(3)过左焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,其中
,其中![]() 是常数,设
是常数,设![]() ,
, ![]() ,计算
,计算![]() 的值(用
的值(用![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() (cosx﹣sinx)sin(x+
(cosx﹣sinx)sin(x+![]() )﹣2asinx+b(a>0).
)﹣2asinx+b(a>0).
(1)若b=1,且对任意![]() , 恒有f(x)>0,求a的取值范围;
, 恒有f(x)>0,求a的取值范围;
(2)若f(x)的最大值为1,最小值为﹣4,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(3+x)+ln(3﹣x).
(Ⅰ)求函数y=f(x)的定义域;
(Ⅱ)判断函数y=f(x)的奇偶性;
(Ⅲ)若f(2m﹣1)<f(m),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有正整数构成的数表如下:
第一行:1
第二行:1 2
第三行:1 1 2 3
第四行:1 1 2 1 1 2 3 4
第五行:1 1 2 1 1 2 3 1 1 2 1 1 2 3 4 5
…… …… ……
第![]() 行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,...,直至按原序抄写第
行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,...,直至按原序抄写第![]() 行,最后添上数
行,最后添上数![]() .(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).
.(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).
将按照上述方式写下的第![]() 个数记作
个数记作![]() (如
(如![]() )
)
(1)用![]() 表示数表第
表示数表第![]() 行的数的个数,求数列
行的数的个数,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)第8行中的数是否超过73个?若是,用![]() 表示第8行中的第73个数,试求
表示第8行中的第73个数,试求![]() 和
和![]() 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(3)令![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com