
【题目】已知函数![]() ,其中
,其中![]() 为自然对数底数.
为自然对数底数.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知![]() ,若函数
,若函数![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)当
(2)当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(3)
.(3)![]()
【解析】
试题分析:(1)根据导数几何意义可求切线斜率:![]() ,再根据点斜式求切线方程为
,再根据点斜式求切线方程为![]() ,即
,即![]() .(2)利用导数求函数单调性,从导函数出发,研究其零点情况:
.(2)利用导数求函数单调性,从导函数出发,研究其零点情况:![]() 当
当![]() 时,
时,![]() ,无零点,函数
,无零点,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,由
时,由![]() 得
得![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增.(3)不等式恒成立问题转化为函数最值问题:
单调递增.(3)不等式恒成立问题转化为函数最值问题:![]() ,当
,当![]() 时,函数
时,函数![]() 无最小值;当
无最小值;当![]() 时,函数
时,函数![]() 最小值为0,
最小值为0,![]() ,此时
,此时![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,
,![]() ,最后研究函数
,最后研究函数![]() 最大值
最大值![]()
试题解析:解:(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() , 2分
, 2分
∴函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() . 4分
. 4分
(2)∵![]() ,
,
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增; 6分
上单调递增; 6分
②当![]() 时,由
时,由![]() 得
得![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
综上,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() . 9分
. 9分
(3)由(2)知,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 不可能恒成立; 10分
不可能恒成立; 10分
当![]() 时,
时,![]() ,此时
,此时![]() ; 11分
; 11分
当![]() 时,由函数
时,由函数![]() 对任意
对任意![]() 都成立,得
都成立,得![]() ,
,
∵![]() ,∴
,∴![]() 13分
13分
∴![]() ,
,
设![]() ,∴
,∴ ![]() ,
,
由于![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
当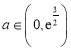 时,
时,![]() ,
,![]() 单调递增;
单调递增;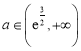 时,
时,![]() ,
,![]() 单调递减.
单调递减.
∴![]() ,即
,即![]() 的最大值为
的最大值为![]() ,
,
此时![]() . 16分
. 16分


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnax﹣ ![]() (a≠0).
(a≠0).
(1)求此函数的单调区间及最值;
(2)求证:对于任意正整数n,均有1+ ![]() +
+ ![]() …+
…+ ![]() ≥ln
≥ln ![]() (e为自然对数的底数).
(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001,002,…,699,700.从中抽取70个样本,如图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( ) 
A.607
B.328
C.253
D.007
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若将其图象向右平移
)的最小正周期是π,若将其图象向右平移 ![]() 个单位后得到的图象关于原点对称,则函数f(x)的图象( )
个单位后得到的图象关于原点对称,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在![]() 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线![]() 上.
上.

(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线![]() 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)数列![]() ,
, ![]() ,
, ![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
, ![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex﹣x﹣1(其中e为自然对数的底数,),若f(x)=0有两根x1 , x2且x1<x2 , 则函数y=(e ![]() ﹣e
﹣e ![]() )(
)( ![]() ﹣m)的值域为 .
﹣m)的值域为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com