
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]() ,
, ![]() .求:
.求:
(1)tan(α+β)的值;
(2)α+2β的大小.
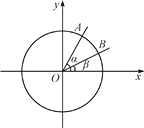
【答案】(1)-3;(2) α+2β=![]() .
.
【解析】试题分析:(1)根据题意,由三角函数的定义可得![]() 与
与![]() 的值,进而可得出
的值,进而可得出![]() 与
与![]() 的值,从而可求
的值,从而可求![]() 与
与![]() 的值就,结合两角和正切公式可得答案;(2)由两角和的正切公式,可得出
的值就,结合两角和正切公式可得答案;(2)由两角和的正切公式,可得出![]() 的值,再根据
的值,再根据![]() 的取值范围,可得出
的取值范围,可得出![]() 的取值范围,进而可得出
的取值范围,进而可得出![]() 的值.
的值.
试题解析:15.解:(1)∵![]() ,从而
,从而![]() .
.
又∵![]() ,∴
,∴![]() . …
. …
利用同角三角函数的基本关系可得sin2(α﹣β)+cos2(α﹣β)=1,且![]() ,
,
解得 由条件得cosα=![]() ,cosβ=
,cosβ=![]() .
.
∵ α,β为锐角,
∴ sinα=![]() =
=![]() ,sinβ=
,sinβ=![]() =
=![]() .
.
因此tanα=![]() =7,tanβ=
=7,tanβ=![]() =
=![]() .
.
(1) tan(α+β)=![]() =
=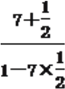 =-3.
=-3.
(2) ∵ tan2β=![]() =
=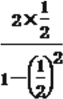 =
=![]() ,
,
∴ tan(α+2β)=![]() =
=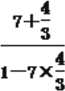 =-1.
=-1.
∵ α,β为锐角,∴ 0<α+2β<![]() ,∴ α+2β=
,∴ α+2β=![]()


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:
【题目】若圆![]() 上有四个不同的点到直线
上有四个不同的点到直线![]() 的距离为2,则
的距离为2,则![]() 的取值范围是( )
的取值范围是( )
A. (-12,8) B. (-8,12) C. (-13,17) D. (-17,13)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知∠A1,∠A2,…,∠An为凸多边形的内角,且lg sin A1+lg sin A2+…+lg sin An=0,则这个多边形是( )
A. 正六边形 B. 梯形
C. 矩形 D. 含锐角的菱形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA = AB = 2,BC = 4, E是PD的中点,
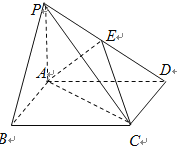
(1)求证: ![]() 平面EAC;
平面EAC;
(2)求证:平面PDC⊥平面PAD;
(3)求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有![]() 个人.把这
个人.把这![]() 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
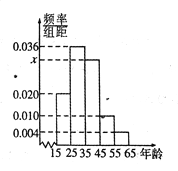
(1)求![]() 和
和![]() 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;
(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,上顶点为
,上顶点为![]() ,下顶点为
,下顶点为![]() ,若直线
,若直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为椭圆
为椭圆![]() 的长轴上的一个动点,过点
的长轴上的一个动点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com