
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.

(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
【答案】(1)![]() (2)直线
(2)直线![]() 与圆
与圆![]() 相切,理由见解析 (3)
相切,理由见解析 (3)![]()
【解析】
(1)根据直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,求出a,b的等量关系即可求解离心率;
,求出a,b的等量关系即可求解离心率;
(2)通过计算可得直线![]() 与以
与以![]() 为直径的圆相切,所以直线
为直径的圆相切,所以直线![]() 与圆
与圆![]() 相切;
相切;
(3)根据面积求出半径,依次列方程组求解参数的值.
解:(1)设椭圆E的焦距为2c(c>0),
因为直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,所以
,所以![]() ,
,
于是![]() ,即
,即![]() ,所以椭圆E的离心率
,所以椭圆E的离心率![]()
(2)由![]() 可设
可设![]() ,
,![]() ,则
,则![]() ,
,
于是![]() 的方程为:
的方程为:![]() ,
,
故![]() 的中点
的中点![]() 到
到![]() 的距离
的距离![]()
![]() ,
,
又以![]() 为直径的圆的半径
为直径的圆的半径![]() ,即有
,即有![]() ,所以直线
,所以直线![]() 与以
与以![]() 为直径的圆相切.
为直径的圆相切.
因为圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称,
对称,
所以直线![]() 与圆
与圆![]() 相切.
相切.
(3)由圆![]() 的面积为
的面积为![]() 知,圆半径为2,从而
知,圆半径为2,从而![]() ,
,
设![]() 的中点
的中点![]() 关于直线
关于直线![]() :
:![]() 的对称点为
的对称点为![]() ,
,
则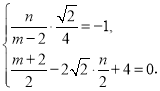 解得
解得![]() .
.
所以,圆![]() 的方程为
的方程为![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)将频率视作概率,从该公司的所有人“运动达人”中任意抽取3个用户,求抽取的用户中女用户人数的分布列及期望.
附:
|
|
|
|
|
|
|
|
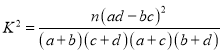
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左右焦点,且椭圆
的左右焦点,且椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过
过![]() 时
时![]() 周长为8.
周长为8.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,是否存在定圆
,是否存在定圆![]() ,使得动直线
,使得动直线![]() 与之相切,若存在写出圆的方程,并求出
与之相切,若存在写出圆的方程,并求出![]() 的面积的取值范围;若不存在,请说明理由.
的面积的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
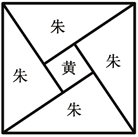
A.2B.4C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,点
中,点![]() 、
、![]() 分别是棱
分别是棱![]() 和
和![]() 的中点,给出下列结论:
的中点,给出下列结论:
①直线![]() 与
与![]() 所成角为
所成角为![]() ;②正方体的所有棱中与直线
;②正方体的所有棱中与直线![]() 异面的有
异面的有![]() 条;③直线
条;③直线![]() 平面
平面![]() ;④平面
;④平面![]() 平面
平面![]() .其中正确的是( )
.其中正确的是( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com