
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率
,离心率![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据题意列出待定系数的方程组,即可求得方程;(2)设![]() 的内切圆的半径为
的内切圆的半径为![]() ,
,
易得![]() 的周长为
的周长为![]() ,所以
,所以![]() ,因此
,因此![]() 最大,
最大,![]() 就最大. 把
就最大. 把![]() 分解为
分解为![]() 和
和![]() ,从而得到
,从而得到![]() ,整理方程组, 求出两根和与两根既即得到面积
,整理方程组, 求出两根和与两根既即得到面积![]() 与
与![]() 的函数关系,通过换元,利用均值不等式即可求得
的函数关系,通过换元,利用均值不等式即可求得![]() 的最大值
的最大值![]() ,此时
,此时![]() .
.
试题解析:(1)由题意可得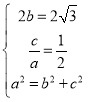 ...................2分
...................2分
解得![]() ..................3分
..................3分
故椭圆的标准方程为![]() ..................... 4分
..................... 4分
(2)设![]() ,设
,设![]() 的内切圆的半径为
的内切圆的半径为![]() ,
,
因为![]() 的周长为
的周长为![]() ,
,![]() ,
,
因此![]() 最大,
最大,![]() 就最大........................6分
就最大........................6分
![]() ,
,
由题意知,直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]() ,
,
由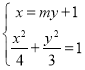 得
得![]() ,
,
所以,![]() .................8分
.................8分
又因直线![]() 与椭圆
与椭圆![]() 交于不同的两点,
交于不同的两点,
故![]() ,即
,即![]() ,则
,则
![]() ............10分
............10分
令![]() ,则
,则![]() ,
,
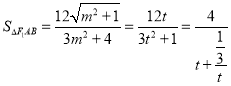 .
.
令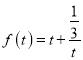 ,由函数的性质可知,函数
,由函数的性质可知,函数![]() 在
在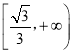 上是单调递增函数,
上是单调递增函数,
即当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
因此有![]() ,所以
,所以![]() ,
,
即当![]() 时,
时,![]() 最大,此时
最大,此时![]() ,
,
故当直线![]() 的方程为
的方程为![]() 时,
时,![]() 内切圆半径的最大值为
内切圆半径的最大值为![]() ...........12分
...........12分


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为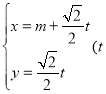 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .且曲线
.且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
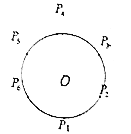
【题目】如图,设![]() 为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量
为单位圆上逆时针均匀分布的六个点,现从这六个点中任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量![]() .
.
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整:并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(2)针对于问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中男生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: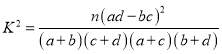 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年5月,我省南昌市遭受连日大暴雨天气,某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票,按照南昌暴雨前后两个时间收集有效投票,暴雨后的投票收集了![]() 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了![]() 份,所得统计结果如下表:
份,所得统计结果如下表:

已知工作人与从所有投票中任取一个,取到“不支持投入”的投票的概率为![]() .
.
(1)求列表中数据的值;
(2)能够有多大的把握认为南昌暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关系?
附: 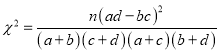
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸离出发地的路程为1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
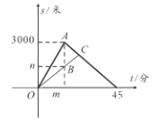
(1)图中![]() ________,
________, ![]() _______;
_______;
(2)求小明和爸爸相遇的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(1)试给出这个常数![]() 的值;
的值;
(2)在(1)所得结论的条件下证明命题![]() ;
;
(3)对于上述命题,某同学正确地猜想了命题![]() :“存在一个常数
:“存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() ,
,![]() 恒成立.”观察命题
恒成立.”观察命题![]() 与命题
与命题![]() 的规律,请猜想与正数
的规律,请猜想与正数![]() ,
,![]() ,
,![]() ,
,![]() 相关的命题.
相关的命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com