
【题目】已知 ![]()
![]() .
.
(1)请写出fn(x)的表达式(不需证明);
(2)设fn(x)的极小值点为Pn(xn , yn),求yn;
(3)设 ![]() ,gn(x)的最大值为a,fn(x)的最小值为b,求b﹣a的最小值.
,gn(x)的最大值为a,fn(x)的最小值为b,求b﹣a的最小值.
【答案】
(1)解:(Ⅰ)fn(x)=(x+n)ex(n∈N*).
(2)解:∵fn′(x)=(x+n+1)ex,
∴当x>﹣(n+1)时,fn′(x)>0;当x<﹣(n+1)时,fn′(x)<0.
∴当x=﹣(n+1)时,fn(x)取得极小值fn[﹣(n+1)]=﹣e﹣(n+1)
,即yn=﹣e﹣(n+1)(n∈N*).
(3)解:∵gn(x)=﹣[x+(n+1)]2+(n﹣3)2
∴a=+(n﹣3)2,
又b=﹣e﹣(n+1),
∴a﹣b=(n﹣3)2+e﹣(n+1),
令h(x)=(x﹣3)2+e﹣(x+1)(x≥0),则h'(x)=2(x﹣3)﹣e﹣(x+1).
∵h'(x)在[0,+∞)单调递增,∴h'(x)≥h'(0)=﹣6﹣e﹣1,
∵h'(3)=﹣e﹣4<0,h'(4)=2﹣e﹣5>0,
∴存在x0∈(3,4)使得h'(x0)=0.
∵h'(x)在[0,+∞)单调递增,
∴当0≤x<x0时,h'(x0)<0;当x>x0时,h'(x0)>0,
即h(x)在[x0,+∞)单调递增,在[0,x0)单调递减,
∴(h(x))min=h(x0),
又∵h(3)=e﹣4,h(4)=1+e﹣5,h(4)>h(3),
∴当n=3时,a﹣b取得最小值e﹣4
【解析】(1)根据导数写出f1(x),f2(x)归纳出fn(x);(2)由(1)知fn(x)的表达式,要求极值点,就要借助导函数,令导函数为0,解出xn , 验证是极值后代入解析式即可求出yn . (3)类比求fn(x)的极小值的过程求出gn(x)的极大值,进而求出最值即可.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx+2 ![]() sinωxcosωx﹣cos2ωx(ω>0),f(x)的图象相邻两条对称轴的距离为
sinωxcosωx﹣cos2ωx(ω>0),f(x)的图象相邻两条对称轴的距离为 ![]() .
.
(1)求f( ![]() )的值;
)的值;
(2)将f(x)的图象上所有点向左平移m(m>0)个长度单位,得到y=g(x)的图象,若y=g(x)图象的一个对称中心为( ![]() ,0),当m取得最小值时,求g(x)的单调递增区间.
,0),当m取得最小值时,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7,且a1+3,3a2 , a3+4构成等差数列.
(1)求数列{an}的通项公式.
(2)令bn=lna3n+1 , n=1,2,…,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:在三棱锥![]() 中,已知底面
中,已知底面![]() 是以
是以![]() 为斜边的等腰直角三角形,且侧棱长
为斜边的等腰直角三角形,且侧棱长![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积等于__________.
的外接球的表面积等于__________.
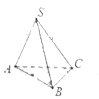
【答案】![]()
【解析】三棱锥![]() 的外接球的球心在SM上(M为AB 中点),球半径设为R,则
的外接球的球心在SM上(M为AB 中点),球半径设为R,则![]()
点睛:涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
【题型】填空题
【结束】
16
【题目】已知斜率![]() 的直线
的直线![]() 过抛物线
过抛物线![]() 的焦点,且与抛物线相交于
的焦点,且与抛物线相交于![]() 、
、![]() 两点,分别过点
两点,分别过点![]() 、
、![]() 若作抛物线的两条切线相交于点
若作抛物线的两条切线相交于点![]() ,则
,则![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
1)若α>β且α、β都是第一象限角,则tanα>tanβ;
2)“对任意x∈R,都有x2≥0”的否定为“存在x0∈R,使得 ![]() <0”;
<0”;
3)已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则(p)∨q为真命题;
4)函数 ![]() 是偶函数.
是偶函数.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: 
(1)BE=EC;
(2)ADDE=2PB2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com