
【题目】如图,在平面直角坐标系xoy中,F为椭圆E:![]() 的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D.
的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D.
(1)当AB=![]() 时,求直线AB的方程;
时,求直线AB的方程;
(2)直线AB交直线x=3于点M,OM与CD交于P,CO与椭圆E交于Q,求证:OM∥DQ.

【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)由题意可设直线AB方程y=k(x-2),则直线CD的方程为![]() ,分别与椭圆方程联立,利用弦长公式可得出|AB|,|CD|,根据AB=
,分别与椭圆方程联立,利用弦长公式可得出|AB|,|CD|,根据AB=![]() 解得k,即可得直线AB方程.(2)将直线AB与直线x=3联立,解得M,可得直线OM方程,将直线OM与直线CD联立,解得P点坐标,将直线CD与椭圆联立,利用根与系数的关系、中点坐标公式可得线段CD的中点坐标,得到与点P重合.又点O是CQ的中点,由三角形中位线即可证明结论.
解得k,即可得直线AB方程.(2)将直线AB与直线x=3联立,解得M,可得直线OM方程,将直线OM与直线CD联立,解得P点坐标,将直线CD与椭圆联立,利用根与系数的关系、中点坐标公式可得线段CD的中点坐标,得到与点P重合.又点O是CQ的中点,由三角形中位线即可证明结论.
(1)由题意可设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() .则直线
.则直线![]() 的方程为:
的方程为:![]() .
.
联立![]() ,化为:
,化为:![]() ,
,
![]() ,
,![]() ,
,
则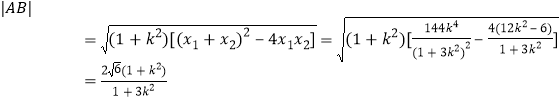 .
.
同理可得: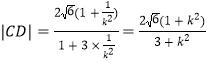 .
.
![]() ,
,![]() .
.
化为:![]() ,解得
,解得![]() .
.
![]() 直线
直线![]() 的方程为:
的方程为:![]() .
.
(2)证明:设直线![]() 的方程为:
的方程为:![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
联立![]() ,解得
,解得![]() .
.
可得直线![]() 的方程:
的方程:![]() ,
,
联立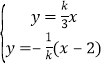 ,解得
,解得![]() .
.
联立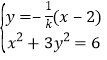 ,化为:
,化为:![]() ,
,
![]() ,可得线段
,可得线段![]() 的中点坐标
的中点坐标![]() ,与点
,与点![]() 重合.
重合.
又点![]() 是
是![]() 的中点,
的中点,![]() ,即
,即![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元,若病人每餐至少需要35单位蛋白质和40单位铁质。试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知![]() 两学习小组各有
两学习小组各有![]() 位同学,每位同学在两场讲座任意选听一场.若
位同学,每位同学在两场讲座任意选听一场.若![]() 组
组![]() 人选听《生活趣味数学》,其余
人选听《生活趣味数学》,其余![]() 人选听《校园舞蹈赏析》;
人选听《校园舞蹈赏析》;![]() 组
组![]() 人选听《生活趣味数学》,其余
人选听《生活趣味数学》,其余![]() 人选听《校园舞蹈赏析》.
人选听《校园舞蹈赏析》.
(1)若从此![]() 人中任意选出
人中任意选出![]() 人,求选出的
人,求选出的![]() 人中恰有
人中恰有![]() 人选听《校园舞蹈赏析》的概率;
人选听《校园舞蹈赏析》的概率;
(2)若从![]() 两组中各任选
两组中各任选![]() 人,设
人,设![]() 为选出的
为选出的![]() 人中选听《生活趣味数学》的人数,求
人中选听《生活趣味数学》的人数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,侧棱PA⊥底面ABCD,且PA=AD,E,F分别是线段PA,PD的中点,H在线段AB上.
(1)求证:PC⊥AF;
(2)若平面PBC∥平面EFH,求证H是AB的中点;
(3)若AD=4,AB=2,求点D到平面PAC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 且
且![]() ,设命题
,设命题![]() :函数
:函数![]() 在
在![]() 上单调递减,命题
上单调递减,命题![]() :对任意实数
:对任意实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(1)写出命题![]() 的否定,并求非
的否定,并求非![]() 为真时,实数
为真时,实数![]() 的取值范围;
的取值范围;
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣ ![]() cosx(a∈R)的图象经过点(
cosx(a∈R)的图象经过点( ![]() ,0).
,0).
(1)求f(x)的最小正周期;
(2)若x∈[ ![]() ,
, ![]() ],求f(x)的取值范围.
],求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() (a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
(a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
A.(3,+∞)
B.(0, ![]() ]
]
C.(1,3)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 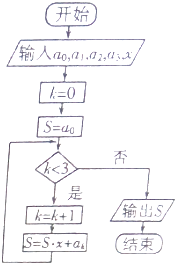
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com